Capítulo 5 Decomposição de Séries Temporais
library(BETS)
library(forecast)
library(lubridate)
library(tidyverse)
library(magrittr)
library(seasonal)Séries Temporais podem exibir uma grande variedade de padrões que podem ser modelados separadamentes, o que pode ajudar o analista a entender melhor os dados e até mesmo a melhorar as previsões.
Já vimos no capítulo introdutório que uma série temporal possui três tipos de padrão: tendência, sazonalidade e ciclo. Se assumirmos que a série segue um modelo aditivo, então, matematicamente, ela pode ser descrita pela equação \(y_t = S_t + T_t + E_t\), onde \(E_t\) é o componente do erro no período \(t\). Se a série for melhor descrita por um modelo multiplicativo, então a equação vira \(y_t = S_t \times T_t \times E_t\).
Para se decidir se uma série segue um modelo aditivo ou multiplicativo (alguns algoritmos já calculam isso internamente), observe se a magnitude dos períodos sazonais ou a variância da tendência cresce conforme o nível (valores absolutos) da série cresce.
Por exemplo:
# simulando uma série de modelo aditivo
set.seed(123)
x <- 1:500 + c(rnorm(250, 50, 25), rnorm(250, 50, 25))
plot(x, type = "l")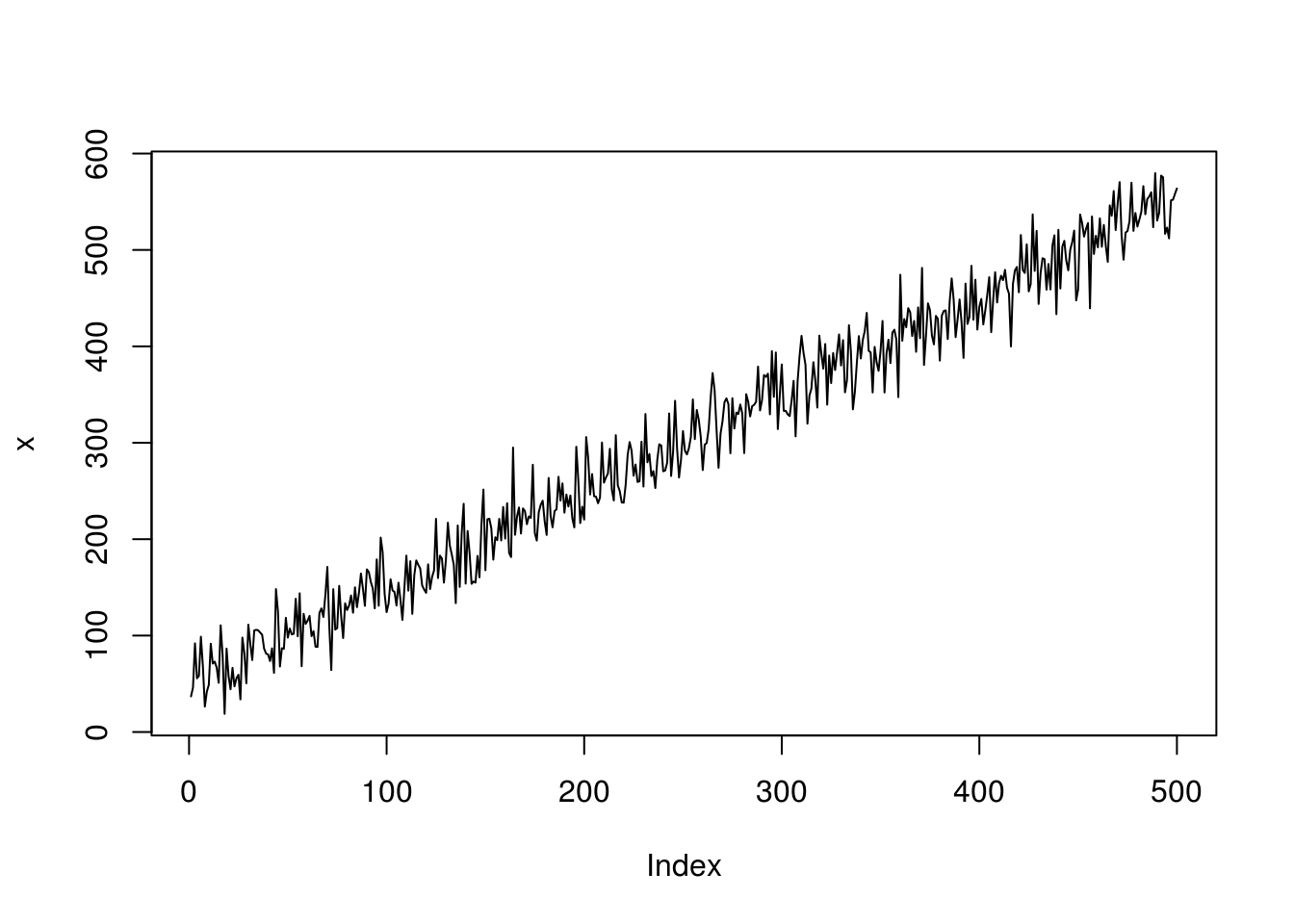
# modelo multiplicativo
a <- rep(1, 500)
b <- 1:500/8
set.seed(123)
x2 <- pmap(list(a, b), rnorm, mean = 0) %>% as.numeric()
x <- 1:500 + x2
plot(x, type = "l")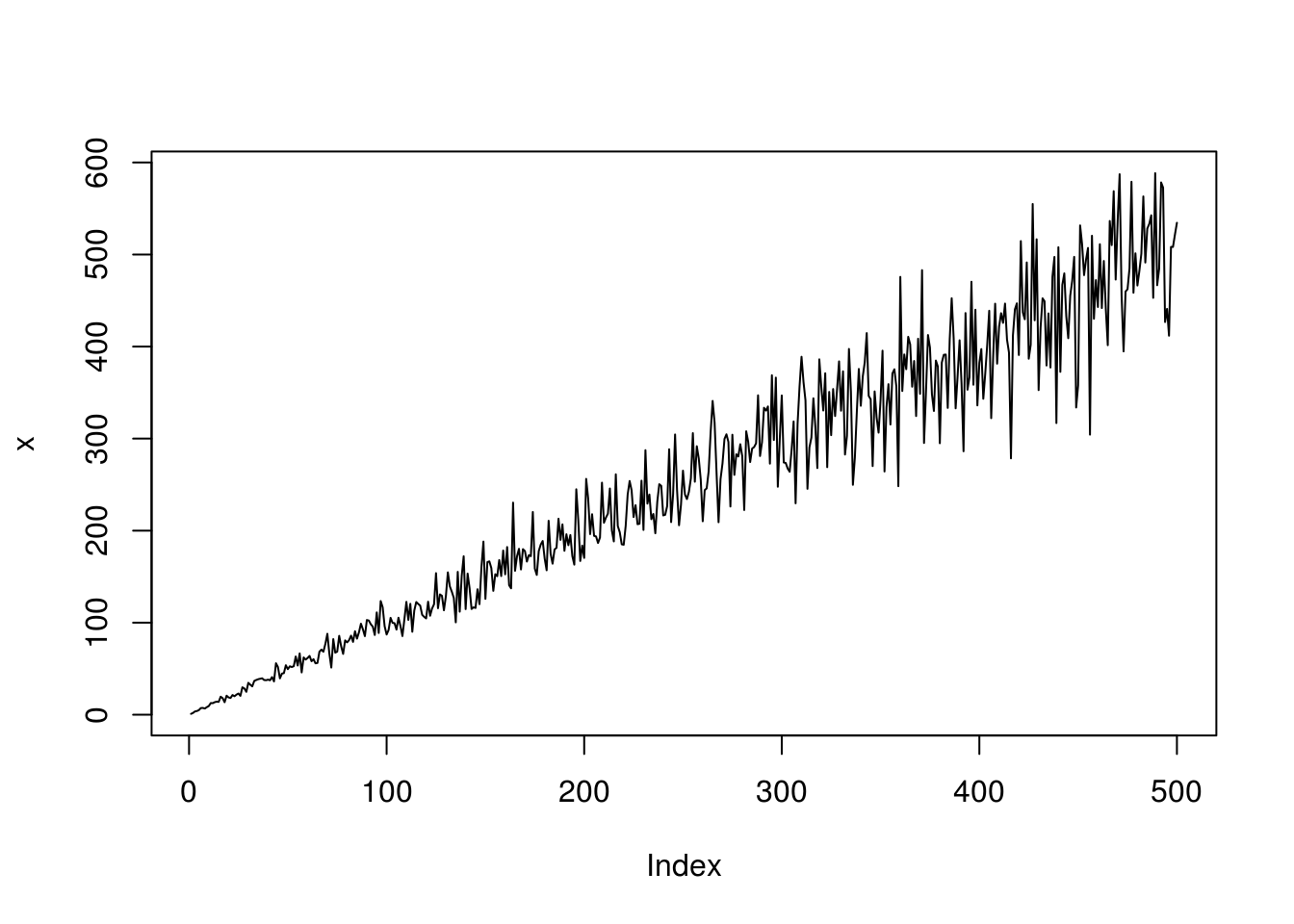
No segundo gráfico, vemos que, para valores maiores da série temporal, a variância dos dados é maior.
5.1 Médias móveis
Embora seja meio datada e tenha dado espaço para técnicas mais avançadas de decomposição, a média móvel é a base de muitos métodos de análises de séries temporais e uma importante etapa para estimar o componente de tendência de uma série.
Vamos voltar a analisar a série temporal baixada por meio do BETS:
energia <- readRDS("data/ts_energia.Rda")
# plotando a serie contra uma media movel de 3 meses
plot(energia)
ma(energia, 3) %>% lines(col = "red", lwd = 1)
# a media movel de 3 meses nao foi suficiente. vamos aumentar o periodo
ma(energia, 12) %>% lines(col = "blue", lwd = 2)
ma(energia, 24) %>% lines(col = "green", lwd = 3)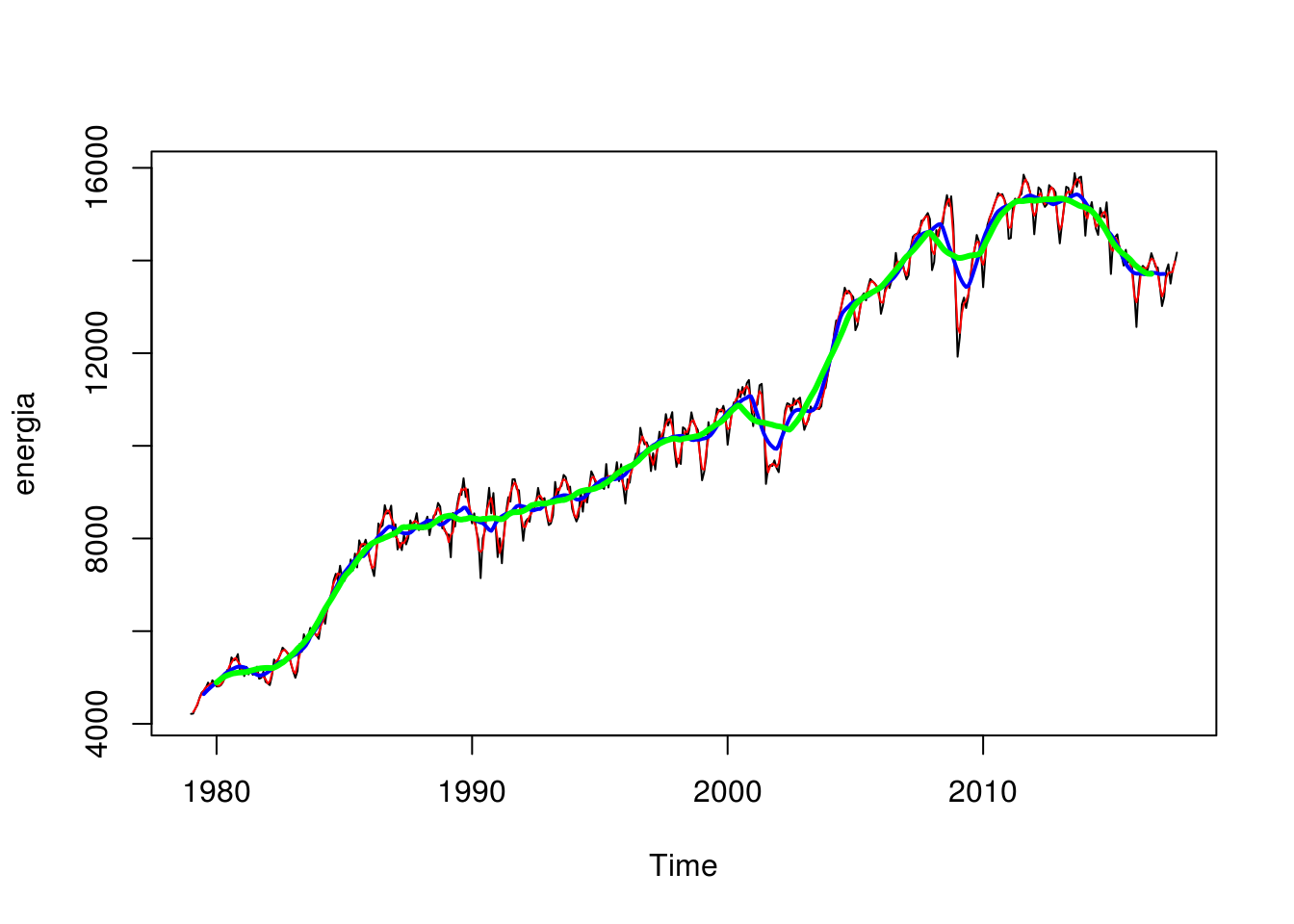
A curva que apresenta menos flutuações sazonais é verde, referente à média móvel de 24 períodos. Mesmo assim, pode-se dizer que essa decomposição não foi satisfatória, devido a curva apresentar perturbações mesmo usando um período longo (24 meses) para sua estimação.
5.2 Decomposição clássica
A técnica de decomposição clássica é um procedimento relativamente simples, mas depende da definição do usuário se a série temporal analisada segue um modelo aditivo ou multiplicativo.
- Calcule a média móvel da série temporal:
# convertendo para dataframe
df_energia <- data.frame(
data = seq.Date(from = as.Date("1979-01-01"), by = "month",
length.out = length(energia)),
st = energia
)
# adicionando a media movel
df_energia$media_movel <- ma(energia, 24)- Remova o componente de tendência da série. Caso seja o modelo seja aditivo, subtraia a série pela tendência. Caso seja multiplicativo, divida.
df_energia$serie_sem_tend_adt <- energia - df_energia$media_movel
df_energia$serie_sem_tend_mult <- energia / df_energia$media_movel- Calcule a média da série sem tendência para cada período sazonal.
# no caso dessa serie de exemplo, que possui frequencia igual a 12,
# um periodo sazonal corresponde aos 12 meses do ano
df_energia %<>%
group_by(mes = month(data)) %>%
mutate(saz_adi = mean(serie_sem_tend_adt, na.rm = TRUE),
saz_mult = mean(serie_sem_tend_mult, na.rm = TRUE)) %>%
ungroup()
# é necessário verificar se os indices sazonais aditivos somam 0 e se os multiplicativos somam 12
df_energia$saz_adi %>% unique %>% sum## [1] 44.28006df_energia$saz_mult %>% unique %>% sum## [1] 12.00097# os indices sazonais nao somam zero, portanto precisamos rescalar o vetor:
df_energia %<>%
mutate(saz_adi = scale(saz_adi)) %>%
ungroup()
# checando novamente
df_energia$saz_adi %>% unique %>% sum## [1] 0.06138936- Calcular o componente de erro (restante)
# se for aditivo, e = y_t - T_t - S_t
df_energia %<>% mutate(
erro_adi = serie_sem_tend_adt - saz_adi,
erro_mult = serie_sem_tend_mult / saz_mult
)Vamos comparar os dois componentes de erro obtidos:
layout(matrix(c(1,1,2,3), 2, 2, byrow = TRUE))
plot(df_energia$erro_adi, type = "l")
lines(df_energia$erro_mult, type = "l", col = "red")
hist(df_energia$erro_adi, main = "Distribuição do erro aditivo")
hist(df_energia$erro_mult, main = "Distribuição do erro multiplicativo")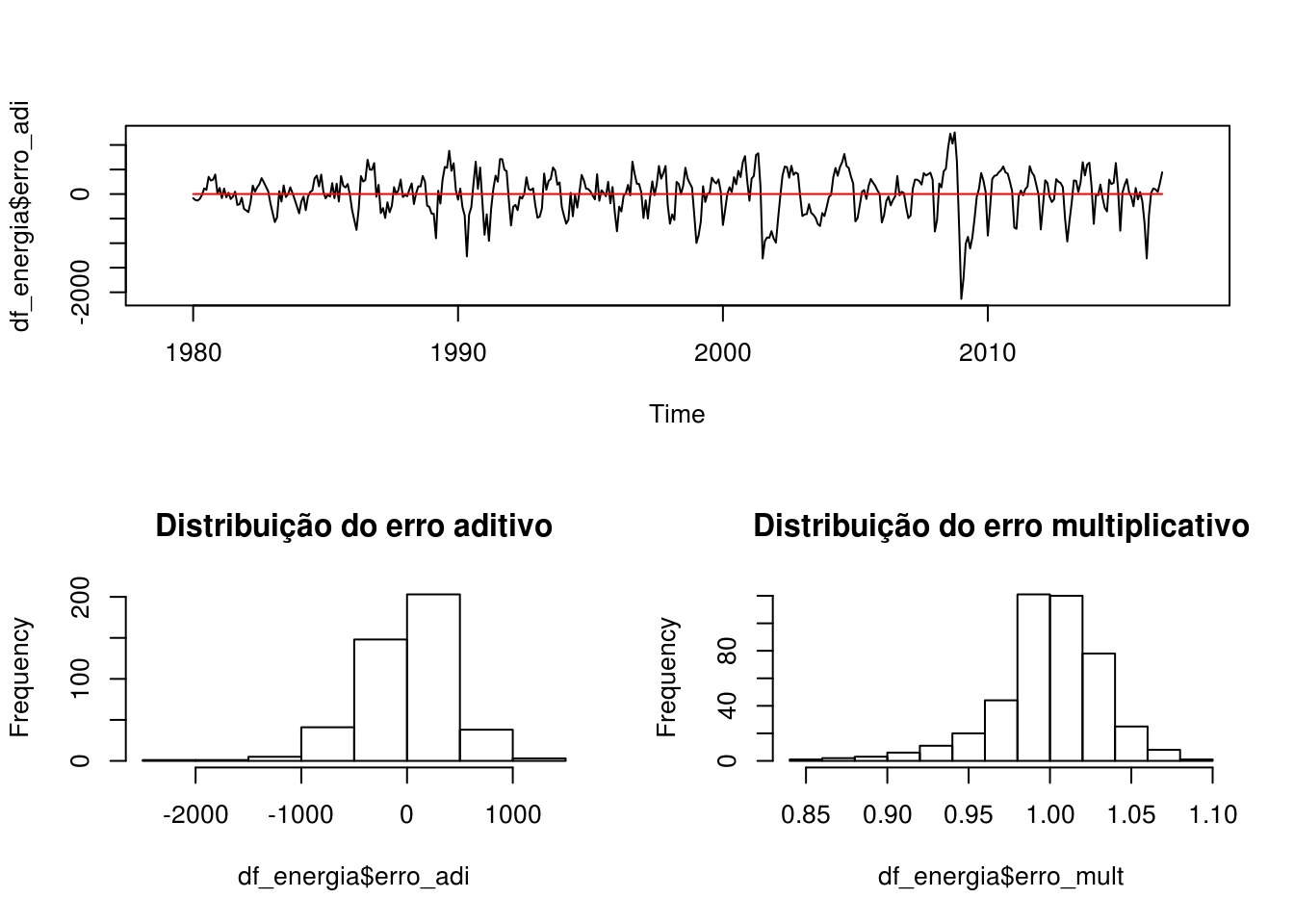
Outro gráfico que pode ser usado para comparar o erro aleatório é o de autocorrelação:
par(mfrow = c(1,2))
df_energia %$% acf(erro_adi, na.action = na.omit)
df_energia %$% acf(erro_mult, na.action = na.omit)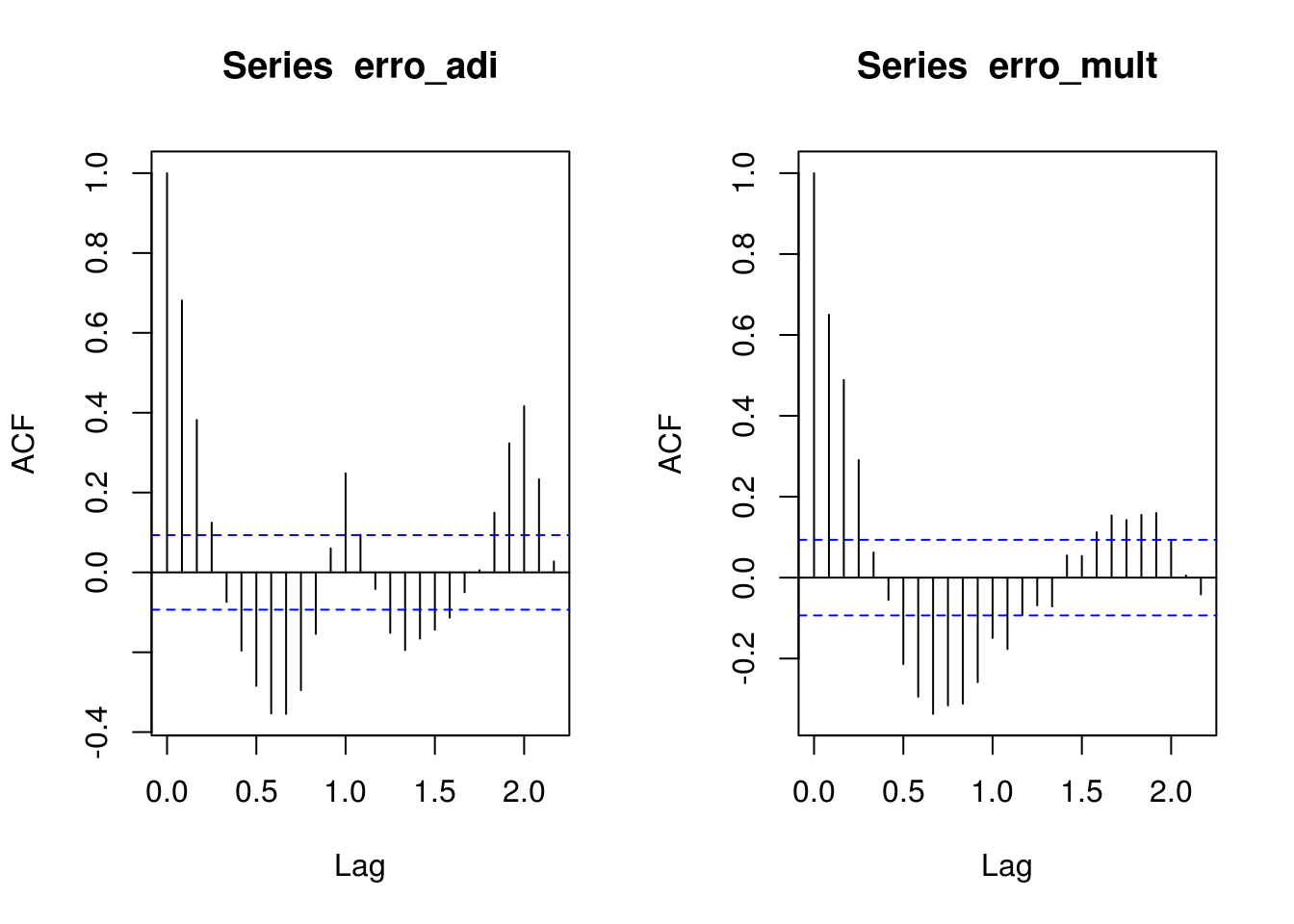
# verificando qual dos dois possui a menor autocorrelacao total
df_energia %$%
acf(erro_adi, na.action = na.omit, plot = FALSE)$acf^2 %>%
sum## [1] 2.666452df_energia %$%
acf(erro_mult, na.action = na.omit, plot = FALSE)$acf^2 %>%
sum## [1] 2.455227Pela análise da autocorrelação, a decomposição multiplicativa parece ser mais apropriada.
5.3 Outros tipos de decomposição
5.3.1 Pacote seasonal
O pacote seasonal, disponível no CRAN, implementa uma interface ao algoritmo e software X-13-ARIMA-SEATS, desenvolvido pelo US Census Bureau. Possui recursos como seleção automática do modelo ARIMA, detecção de outliers e suporte para feriados definidos pelo usuário, como Carnaval e Páscoa.
Um rápido uso do pacote seasonal é mostrado abaixo:
m <- seas(energia)
# resumo sobre o modelo
summary(m)##
## Call:
## seas(x = energia)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## Leap Year 7.020e+01 5.445e+01 1.289 0.19732
## Mon -2.497e+01 1.730e+01 -1.443 0.14899
## Tue -1.625e+01 1.734e+01 -0.937 0.34873
## Wed -5.557e+01 1.737e+01 -3.199 0.00138 **
## Thu 8.803e+01 1.744e+01 5.048 4.47e-07 ***
## Fri -3.498e+01 1.756e+01 -1.992 0.04638 *
## Sat 1.828e+01 1.736e+01 1.053 0.29235
## Easter[15] -1.118e+02 3.733e+01 -2.996 0.00274 **
## AO1990.May -9.159e+02 1.583e+02 -5.786 7.22e-09 ***
## LS2001.Jul -1.697e+03 1.919e+02 -8.843 < 2e-16 ***
## LS2003.Dec 8.556e+02 1.922e+02 4.453 8.49e-06 ***
## AO2008.Dec 9.660e+02 1.990e+02 4.855 1.21e-06 ***
## LS2008.Dec -2.080e+03 2.416e+02 -8.611 < 2e-16 ***
## AR-Nonseasonal-01 -2.790e-01 4.473e-02 -6.239 4.41e-10 ***
## MA-Seasonal-12 7.619e-01 3.152e-02 24.175 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## SEATS adj. ARIMA: (1 1 0)(0 1 1) Obs.: 464 Transform: none
## AICc: 6151, BIC: 6215 QS (no seasonality in final):0.555
## Box-Ljung (no autocorr.): 34.1 . Shapiro (normality): 0.9899 **
## Messages generated by X-13:
## Notes:
## - Unable to test LS2009.Jan due to regression matrix
## singularity.
## - Unable to test LS2001.Jun due to regression matrix
## singularity.
## - Unable to test LS2009.Jan due to regression matrix
## singularity.# plotando o modelo
plot(m)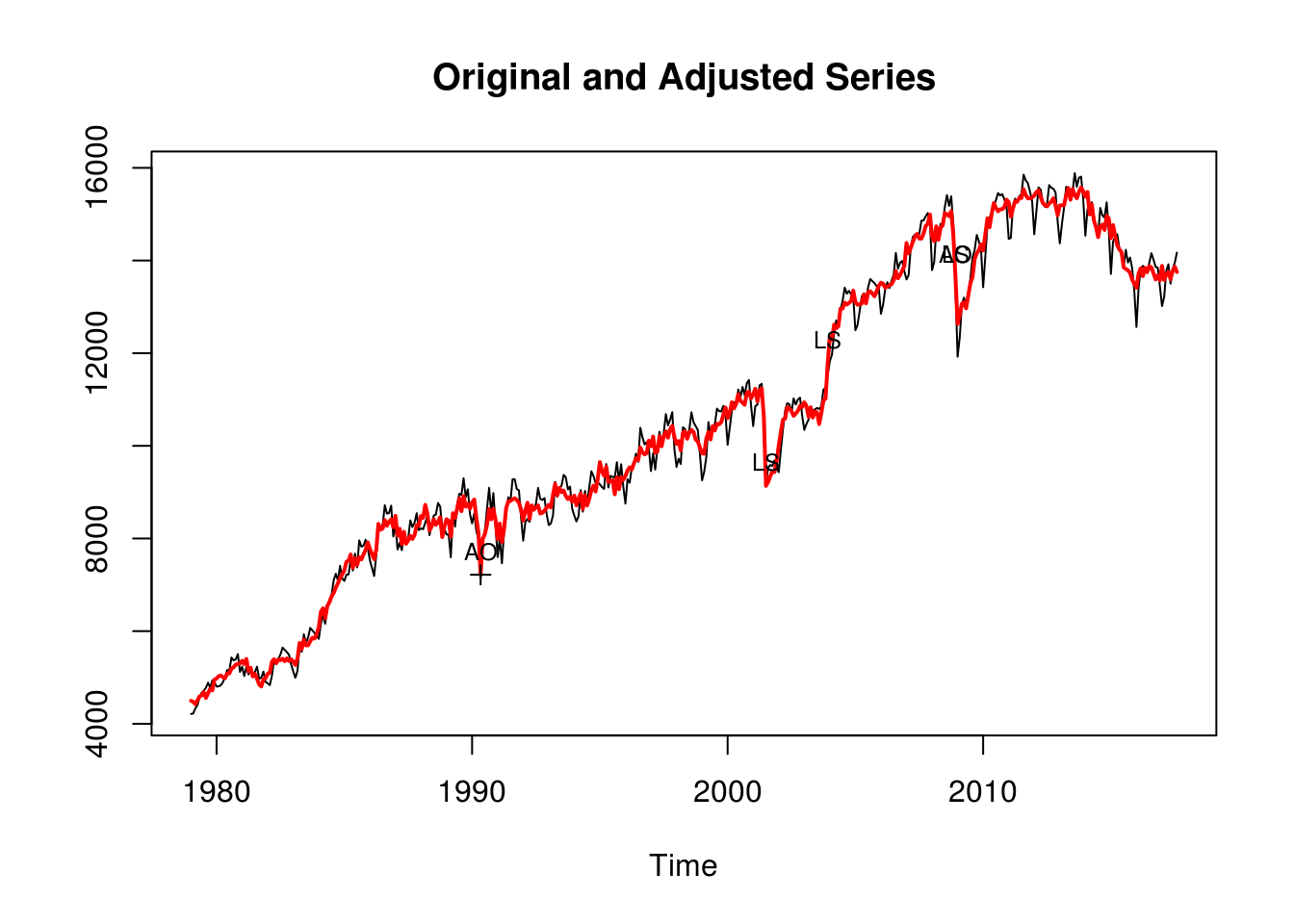
# retornando as componentes individuais da serie:
final(m) %>% head(20) # serie sem tendencia## Jan Feb Mar Apr May Jun Jul
## 1979 4497.204 4476.151 4425.449 4506.397 4593.717 4614.867 4684.848
## 1980 4978.268 5028.129 5044.723 5004.944 4984.573 5088.178 5087.665
## Aug Sep Oct Nov Dec
## 1979 4557.699 4660.105 4755.526 4721.976 4953.909
## 1980 5192.940trend(m) %>% head(20) # tendencia da serie## Jan Feb Mar Apr May Jun Jul
## 1979 4474.778 4469.107 4468.870 4511.471 4573.757 4619.751 4630.539
## 1980 4976.258 5015.414 5025.123 5014.482 5022.780 5063.216 5115.465
## Aug Sep Oct Nov Dec
## 1979 4626.196 4662.275 4723.461 4796.778 4896.599
## 1980 5172.743irregular(m) %>% head(20) # erro aleatorio## Jan Feb Mar Apr May Jun
## 1979 19.036021 3.444931 -35.228172 -6.569534 14.580363 5.446363
## 1980 10.372929 11.667839 16.790921 -10.372967 -28.680835 12.428619
## Jul Aug Sep Oct Nov Dec
## 1979 35.064941 -49.532004 -5.437489 17.297197 -49.988443 37.101743
## 1980 -16.551551 11.9444695.3.2 Decomposição STL
O método STL funciona apenas para decomposições aditivas. Aplicá-la no R é muito fácil, usando a função stl:
energia %>%
stl(s.window = "periodic") %>% #raramente este argumento sera diferente
plot