Capítulo 8 Outros Métodos
library(fpp)
library(forecast)
library(tidyverse)
library(vars)
library(mafs)Forecasting é um assunto amplo demais para ser compreendido em algumas poucas horas. Existem dezenas de métodos de previsão diferentes, cada um apropriada a situações específicas. Além das técnicas clássicas apresentadas aqui, existem ainda algumas outras que vem ganhando destaque.
8.1 Modelos de regressão dinâmica
Suponha que você tenha em mãos dados “externos” à série temporal em análise que podem ser relevantes, como indicadores macroeconômicos, feriados, competidores, mudanças na lei, etc. Este subcapítulo aborda como incorporar dados externos (também chamados de regressores externos) a um modelo ARIMA.
data("usconsumption")
plot(usconsumption)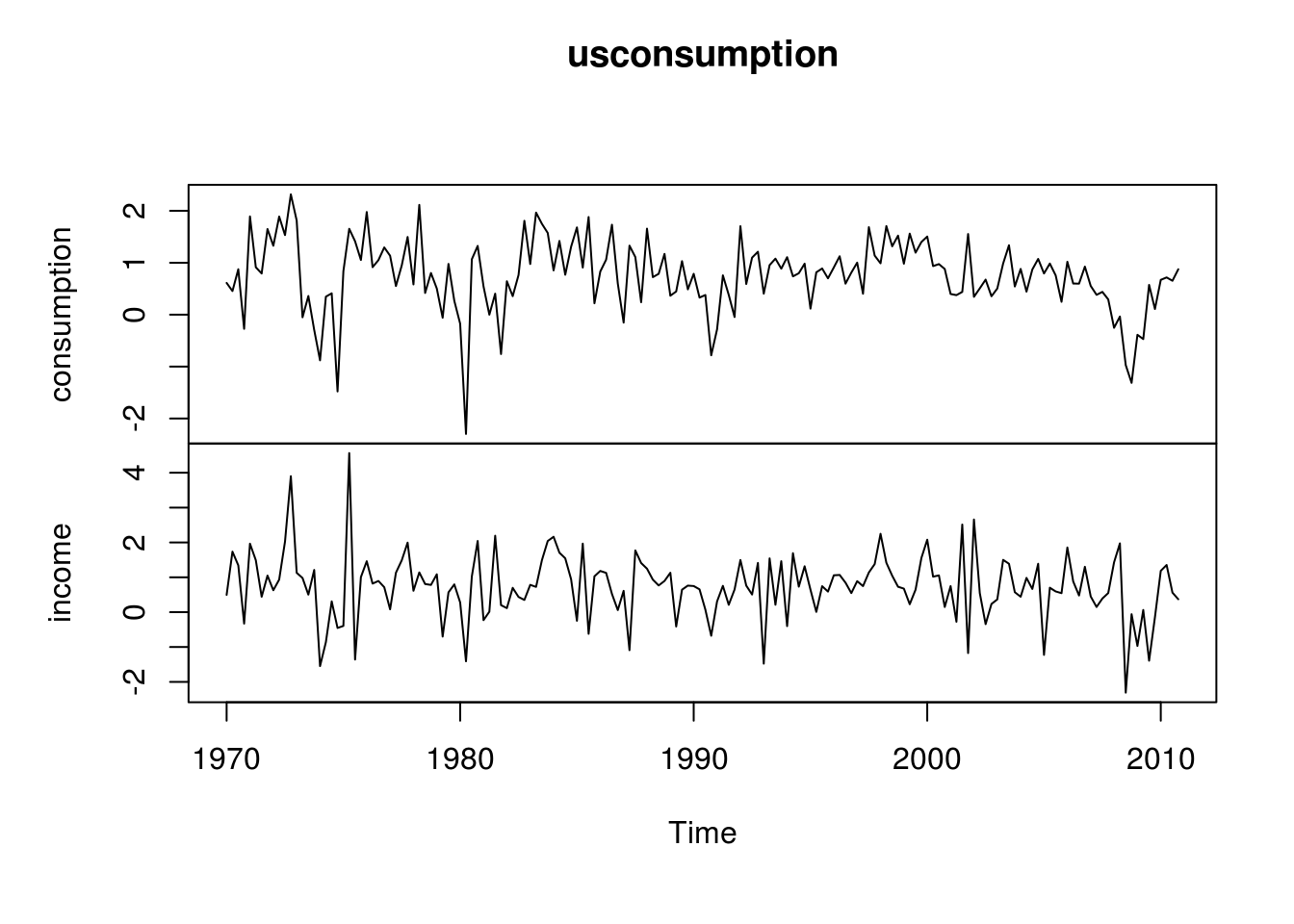
O dataset acima se refere à mudanças percentuais trimestrais em gastos pessoais (consumption) e na renda disponível das famílias americanas entre 1970 e 2010. Naturalmente, espera-se que as duas séries sejam correlacionadas:
cor(usconsumption[,1], usconsumption[, 2])## [1] 0.4320562Embora 0,43 não seja um valor muito significativo, vamos continuar com essa hipótese e tentar medir o efeito instantâneo que a variável explanatória renda possui na variável resposta consumo.
Antes de ajustar um modelo ARIMA nessa série de consumo, será necessário a diferenciar?
Vamos então medir a qualidade do ajuste de três modelos ARIMA: O primeiro sem regressor externo e com seleção automática do modelo ARIMA, o segundo usando o modelo ARIMA do primeiro e com regressor externo e o terceiro com seleção automática do modelo e com regressor externo:
consumo <- usconsumption[,1]
renda <- usconsumption[,2]
(ajuste1 <- auto.arima(consumo, seasonal = FALSE))## Series: consumo
## ARIMA(0,0,3) with non-zero mean
##
## Coefficients:
## ma1 ma2 ma3 mean
## 0.2542 0.2260 0.2695 0.7562
## s.e. 0.0767 0.0779 0.0692 0.0844
##
## sigma^2 estimated as 0.3953: log likelihood=-154.73
## AIC=319.46 AICc=319.84 BIC=334.96(ajuste2 <- Arima(consumo, order = c(0, 0, 3), xreg = renda))## Series: consumo
## Regression with ARIMA(0,0,3) errors
##
## Coefficients:
## ma1 ma2 ma3 intercept renda
## 0.1153 0.2778 0.1440 0.5740 0.2464
## s.e. 0.0859 0.0760 0.0766 0.0816 0.0564
##
## sigma^2 estimated as 0.3554: log likelihood=-145.44
## AIC=302.88 AICc=303.42 BIC=321.48(ajuste3 <- auto.arima(consumo, xreg = renda, seasonal = FALSE))## Series: consumo
## Regression with ARIMA(1,0,2) errors
##
## Coefficients:
## ar1 ma1 ma2 intercept xreg
## 0.6516 -0.5440 0.2187 0.5750 0.2420
## s.e. 0.1468 0.1576 0.0790 0.0951 0.0513
##
## sigma^2 estimated as 0.3502: log likelihood=-144.27
## AIC=300.54 AICc=301.08 BIC=319.14Se usarmos a métrica AICc como referência, o melhor modelo ajustado é o terceiro. Observe que, ao adicionar um regressor externo ao modelo, o modelo ARIMA passa a ser diferente.
Como seria então a previsão de um modelo que possui um regressor externo? Existem algumas possibilidades, sendo a mais simples prever o regressor usando sua própria média histórica:
forecast(ajuste3, xreg = rep(mean(renda), 12)) %>% autoplot()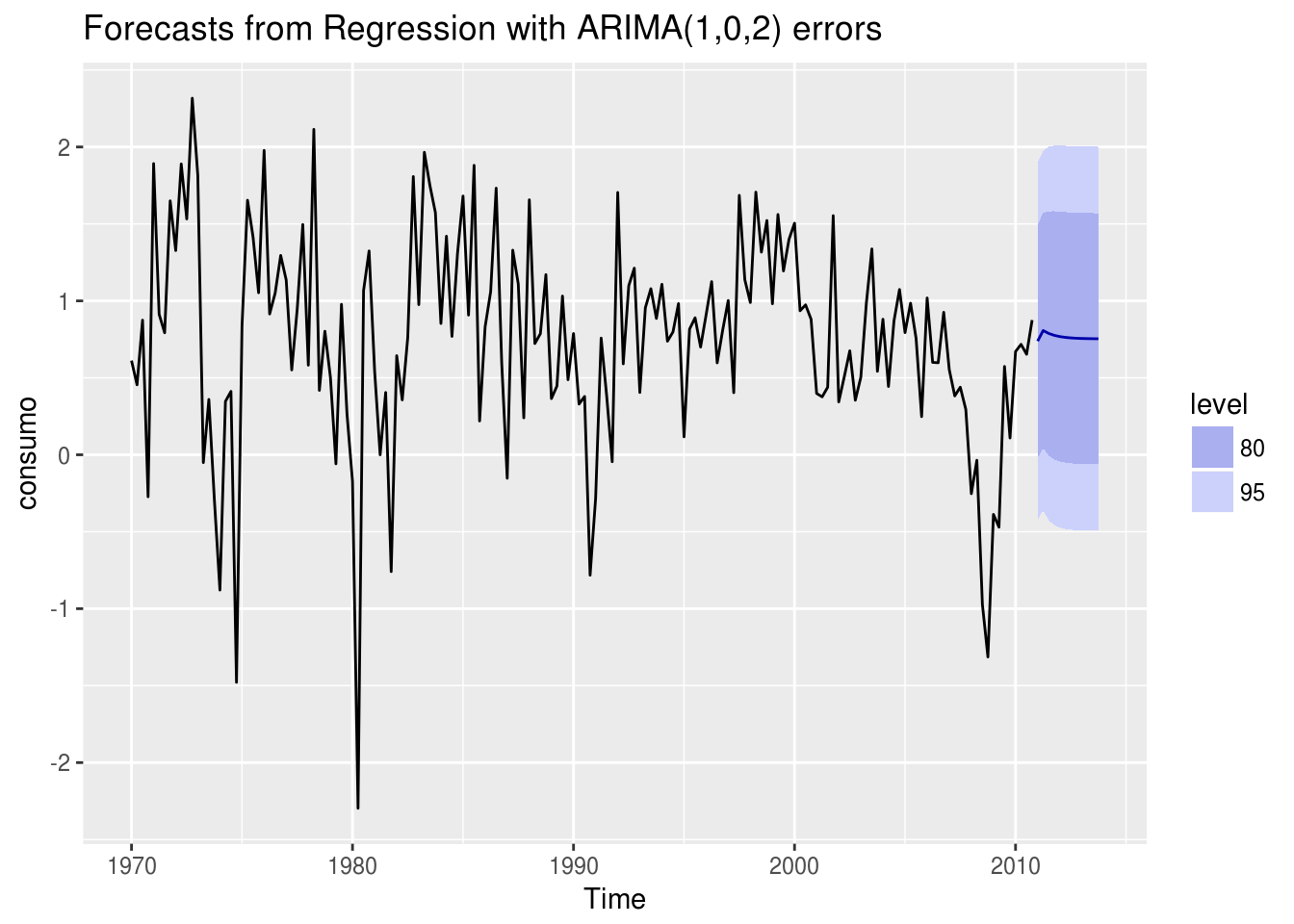
8.2 Modelo de Vetores Autoregressivos (VAR)
Suponha a hipótese de que haja uma relação de mão-dupla entre as duas variáveis analisadas acima. Isto é, não só a renda influencia o consumo como o consumo influencia a renda (pense no aumento da atividade econômica no Natal e os empregos temporários). Esse tipo de problema pode ser chamado de relacionamento bidirecional e é um exemplo de uso dos modelos VAR.
Os modelos VAR foram criados com o objetivo de desenvolver modelos dinâmicos com o mínimo de restrições, nos quais todas as variáveis fossem tratadas como endógenas. Esses modelos examinam relações lineares entre cada variável e os valores defasados (os lags) entre cada variável e os valores defasados dela própria e de todas as variáveis. As únicas restrições impostas pelo modelo são a quantidade de variáveis a incluir ea quantidade de lags, que pode ser definido usando testes estatísticos.
Modelos VAR são aplicados, entre outros, pelo Banco Central do Brasil para gerar previsões para o IPCA. Algumas variáveis usadas nos modelos do BCB são a variação da taxa de juros real, a variação cambinal nominal e a inflação dos pre;cos livres.
Nos modelos VAR, o conjunto de variáveis é tratado de forma que cada uma influencia a outra. Matematicamente, para um conjunto de duas variáveis \(y_1\) e \(y_2\), temos:
\(y_{1, t}= c_1 + \phi_{11,1}y_{1,t-1} + \phi_{12,1}y_{2,t-1} + e_{1,t}\) \(y_{2, t}= c_2 + \phi_{21,1}y_{1,t-1} + \phi_{22,1}y_{2,t-1} + e_{2,t}\)
Pode-se observar que um um modelo VAR é uma generalização do modelo autoregressivo estudado antes e que contem uma equação para cada variável. O termo \(\phi{ii,l}\) se refere a influência do lag \(l\) da variável \(y_i\) nela mesma, enquanto o termo \(\phi{ij,l}\) se refere a influência do lag \(l\) da variável \(y_j\) na variável \(y_i\).
No R, o modelo VAR são implementados pelo pacote vars. O procedimento é o seguinte:
# 1 Decidir a quantidade de lags usados no modelo
VARselect(usconsumption, lag.max = 8, type = "const")## $selection
## AIC(n) HQ(n) SC(n) FPE(n)
## 5 1 1 5
##
## $criteria
## 1 2 3 4 5 6
## AIC(n) -1.2686075 -1.2602950 -1.3053739 -1.3167512 -1.3285567 -1.2932806
## HQ(n) -1.2209645 -1.1808899 -1.1942068 -1.1738220 -1.1538655 -1.0868274
## SC(n) -1.1513054 -1.0647915 -1.0316689 -0.9648447 -0.8984488 -0.7849713
## FPE(n) 0.2812256 0.2835828 0.2711039 0.2680733 0.2649835 0.2745819
## 7 8
## AIC(n) -1.2677759 -1.2518870
## HQ(n) -1.0295607 -0.9819096
## SC(n) -0.6812652 -0.5871748
## FPE(n) 0.2817926 0.2864621# 2 Ajustar o modelo com a quantidade de lags escolhida
var.model <- VAR(usconsumption, p = 1, type = "const")
# 3 Testar se os resíduos do modelo não são correlacionados
serial.test(var.model, lags.pt = 10, type = "PT.asymptotic")##
## Portmanteau Test (asymptotic)
##
## data: Residuals of VAR object var.model
## Chi-squared = 55.082, df = 36, p-value = 0.02182# 4 Repetir o procedimento variando o numero de lags até a hipotese nula puder ser rejeitada
var.model <- VAR(usconsumption, p = 2, type = "const")
serial.test(var.model, lags.pt = 10, type = "PT.asymptotic")##
## Portmanteau Test (asymptotic)
##
## data: Residuals of VAR object var.model
## Chi-squared = 49.447, df = 32, p-value = 0.02518var.model <- VAR(usconsumption, p = 3, type = "const")
serial.test(var.model, lags.pt = 10, type = "PT.asymptotic")##
## Portmanteau Test (asymptotic)
##
## data: Residuals of VAR object var.model
## Chi-squared = 33.384, df = 28, p-value = 0.2219# 5 Analisar o output do modelo
summary(var.model)##
## VAR Estimation Results:
## =========================
## Endogenous variables: consumption, income
## Deterministic variables: const
## Sample size: 161
## Log Likelihood: -338.797
## Roots of the characteristic polynomial:
## 0.7666 0.5529 0.524 0.524 0.3181 0.3181
## Call:
## VAR(y = usconsumption, p = 3, type = "const")
##
##
## Estimation results for equation consumption:
## ============================================
## consumption = consumption.l1 + income.l1 + consumption.l2 + income.l2 + consumption.l3 + income.l3 + const
##
## Estimate Std. Error t value Pr(>|t|)
## consumption.l1 0.22280 0.08580 2.597 0.010326 *
## income.l1 0.04037 0.06230 0.648 0.518003
## consumption.l2 0.20142 0.09000 2.238 0.026650 *
## income.l2 -0.09830 0.06411 -1.533 0.127267
## consumption.l3 0.23512 0.08824 2.665 0.008530 **
## income.l3 -0.02416 0.06139 -0.394 0.694427
## const 0.31972 0.09119 3.506 0.000596 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.6304 on 154 degrees of freedom
## Multiple R-Squared: 0.2183, Adjusted R-squared: 0.1878
## F-statistic: 7.166 on 6 and 154 DF, p-value: 9.384e-07
##
##
## Estimation results for equation income:
## =======================================
## income = consumption.l1 + income.l1 + consumption.l2 + income.l2 + consumption.l3 + income.l3 + const
##
## Estimate Std. Error t value Pr(>|t|)
## consumption.l1 0.48705 0.11637 4.186 4.77e-05 ***
## income.l1 -0.24881 0.08450 -2.945 0.003736 **
## consumption.l2 0.03222 0.12206 0.264 0.792135
## income.l2 -0.11112 0.08695 -1.278 0.203170
## consumption.l3 0.40297 0.11967 3.367 0.000959 ***
## income.l3 -0.09150 0.08326 -1.099 0.273484
## const 0.36280 0.12368 2.933 0.003865 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Residual standard error: 0.855 on 154 degrees of freedom
## Multiple R-Squared: 0.2112, Adjusted R-squared: 0.1805
## F-statistic: 6.873 on 6 and 154 DF, p-value: 1.758e-06
##
##
##
## Covariance matrix of residuals:
## consumption income
## consumption 0.3974 0.1961
## income 0.1961 0.7310
##
## Correlation matrix of residuals:
## consumption income
## consumption 1.0000 0.3639
## income 0.3639 1.0000var.model %>% forecast(h = 4 * 2) %>% autoplot()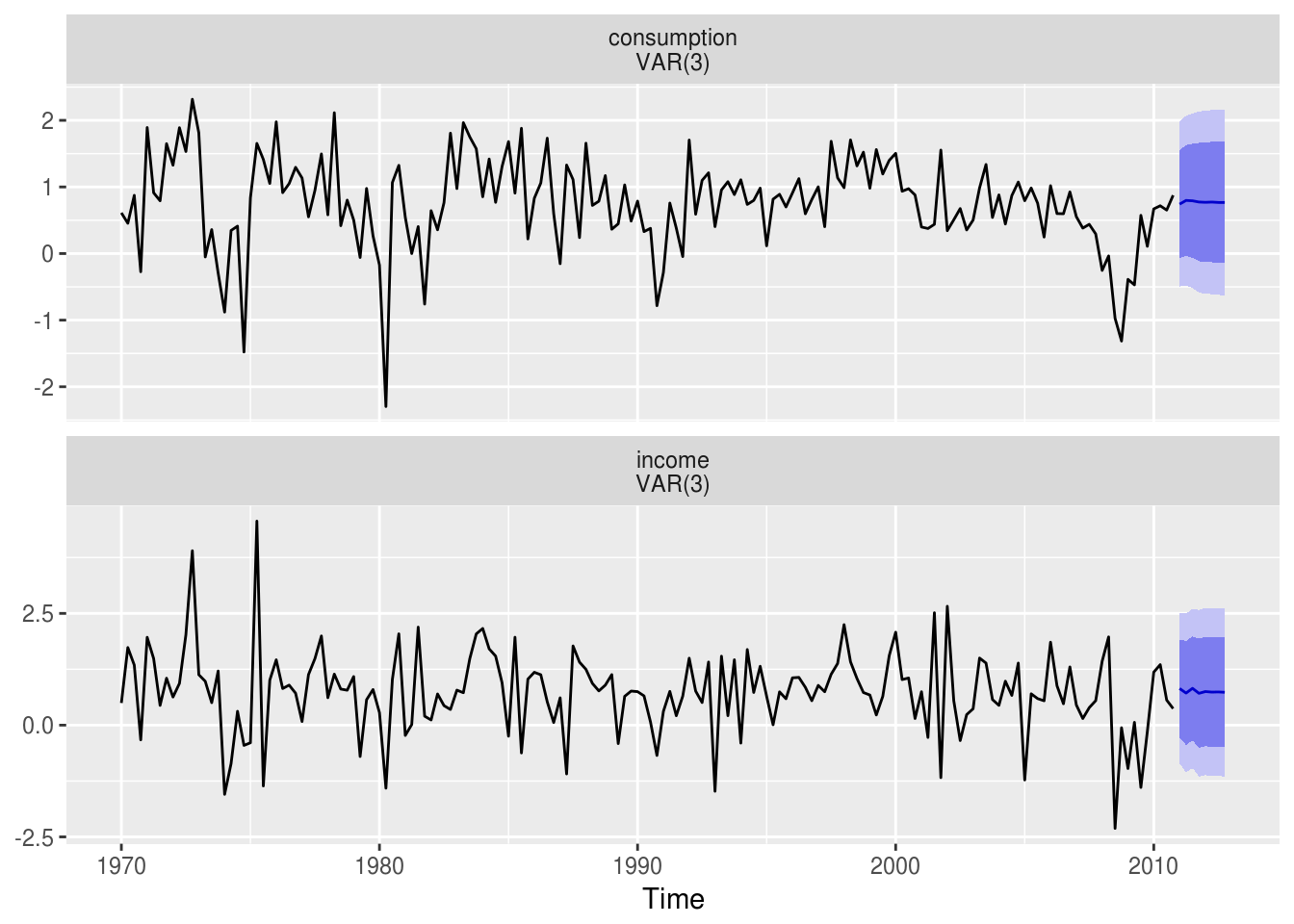
8.3 Redes Neurais
Redes neurais artificiais são métodos de previsão baseados em modelos matemáticos do cérebro humano. Permitem relacionamentos não-lineares complexos entre a variável dependente e a independente.
Uma rede neural pode ser interpretada como uma rede de neurônios organizados em camadas. Os preditores ou inputs formam a camada de baixo e as previsões ou outputs formam a camada de cima. As camadas intermediárias, que podem existir ou não, são chamadas de ocultas.
Cada preditor tem um coeficiente associado a ele, chamado de peso. Inicialmente, os pesos atribuídos aos inputs são valores aleatórios que são atualizados a medida em que a rede neural utiliza um algoritmo de aprendizagem para minimizar uma função de custo do modelo, que corresponde a uma métrica de erro.
A formulação matemática de uma rede neural é razoavelmente complexa. Contudo, ajustá-la em uma série temporal é bem simples:
energia <- readRDS("data/ts_energia.Rda")
mod.rn <- nnetar(energia) %>% forecast(h = 36)
autoplot(mod.rn)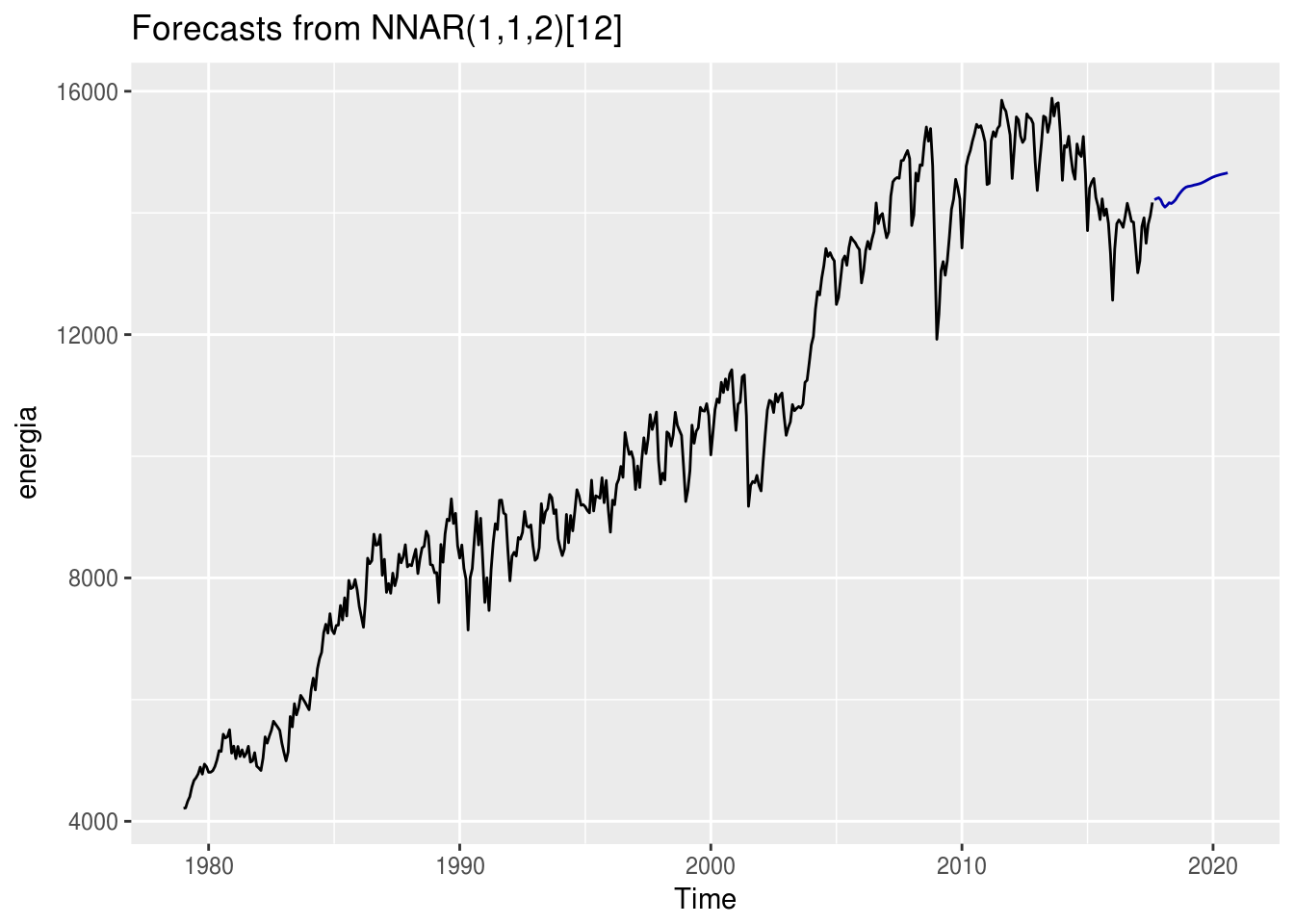
8.4 Pacote mafs
O pacote mafs é basicamente um atalho para o pacote forecast. Sua função principal é select_forecast(), que recebe uma série temporal como input, divide-a em séries de treino e teste, ajusta 18 modelos diferentes no conjunto de treino, mede sua acurácia em relação ao conjunto de teste, seleciona o melhor modelo de acordo com a métrica de erro escolhida pelo usuário e retorna os resultados dos modelos ajustados e os valores previstos para o futuro.
Um exemplo de uso:
system.time({
mod.mafs <- select_forecast(energia, test_size = 24, horizon = 24, error = "MAPE")
})## user system elapsed
## 140.008 191.116 151.538A função select_forecast() retorna como output uma lista de três elementos:
- O resultado da acurácia dos modelos na série de teste;
mod.mafs$df_models %>%
arrange(MAPE) %>%
knitr::kable()| model | ME | RMSE | MAE | MPE | MAPE | MASE | ACF1 | best_model | runtime_model |
|---|---|---|---|---|---|---|---|---|---|
| bats | -142.16876 | 215.2362 | 167.1292 | -1.0566642 | 1.236820 | 0.2955423 | 0.3443626 | bats | 8.306 |
| ets | 19.27086 | 219.3890 | 178.7047 | 0.1182144 | 1.310097 | 0.3160119 | 0.5622831 | bats | 2.725 |
| tbats | -140.17403 | 248.3945 | 184.2845 | -1.0487086 | 1.367947 | 0.3258789 | 0.2451438 | bats | 20.028 |
| thetaf | -237.25935 | 314.1288 | 270.3844 | -1.7481951 | 1.988302 | 0.4781333 | 0.2903167 | bats | 0.037 |
| hybrid | -314.83428 | 373.7628 | 314.8343 | -2.3337677 | 2.333768 | 0.5567361 | 0.4380299 | bats | 23.906 |
| auto.arima | 153.46898 | 446.2479 | 355.0296 | 1.0631006 | 2.587665 | 0.6278154 | 0.7643967 | bats | 5.599 |
| stlm_ets | -405.82082 | 449.6526 | 405.8208 | -2.9749079 | 2.974908 | 0.7176319 | 0.4093080 | bats | 0.125 |
| stlm_arima | -405.83039 | 449.6597 | 405.8304 | -2.9749778 | 2.974978 | 0.7176488 | 0.4092911 | bats | 0.208 |
| splinef | -443.08136 | 579.2958 | 443.5010 | -3.3109120 | 3.313876 | 0.7842634 | 0.5172655 | bats | 8.137 |
| StructTS | -486.68060 | 535.3663 | 486.6806 | -3.5709380 | 3.570938 | 0.8606200 | 0.4522487 | bats | 1.512 |
| naive | -518.45833 | 640.0267 | 518.4583 | -3.8618757 | 3.861876 | 0.9168140 | 0.5196504 | bats | 0.004 |
| rwf | -518.45833 | 640.0267 | 518.4583 | -3.8618757 | 3.861876 | 0.9168140 | 0.5196504 | bats | 0.005 |
| snaive | -744.79167 | 868.8174 | 754.3750 | -5.4768661 | 5.545570 | 1.3339965 | 0.6516216 | bats | 0.005 |
| rwf_drift | -803.65196 | 893.9092 | 803.6520 | -5.9396902 | 5.939690 | 1.4211352 | 0.5547169 | bats | 0.007 |
| croston | -862.80265 | 940.8845 | 862.8027 | -6.3749982 | 6.374998 | 1.5257341 | 0.5196504 | bats | 6.113 |
| nnetar | -1364.02882 | 1461.1896 | 1364.0288 | -10.0096825 | 10.009683 | 2.4120757 | 0.7618458 | bats | 2.302 |
| tslm | -2365.22601 | 2377.3242 | 2365.2260 | -17.2924710 | 17.292471 | 4.1825394 | 0.4967107 | bats | 0.024 |
| meanf | 3443.18939 | 3463.5803 | 3443.1894 | 25.0513535 | 25.051354 | 6.0887522 | 0.5196504 | bats | 0.001 |
- A previsão gerada pelo melhor modelo (no caso, o auto.arima):
mod.mafs$best_forecast %>% autoplot()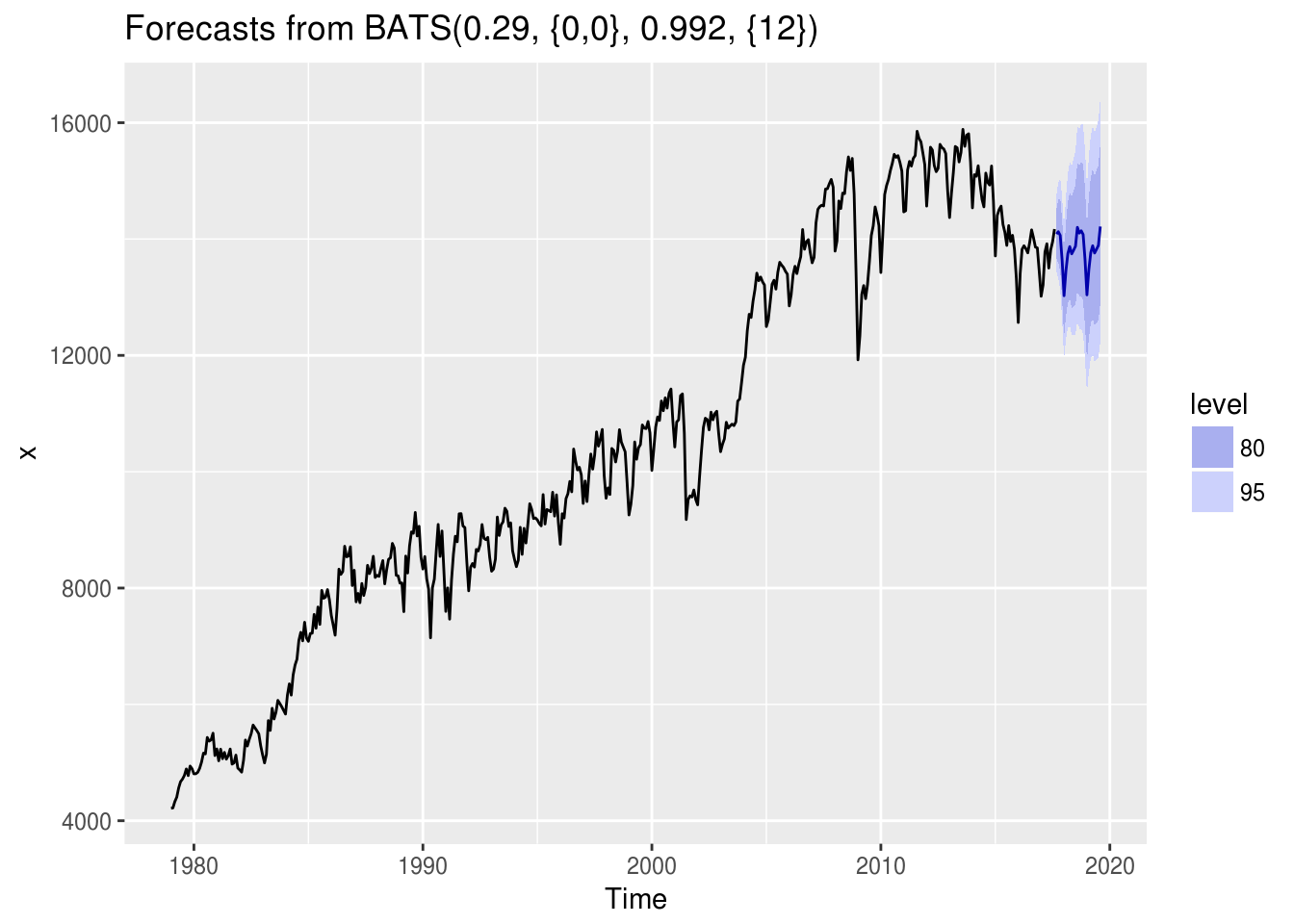
- A comparação entre os valores da série de teste e da previsão resultante do modelo na série de treino:
mod.mafs$df_comparison %>% knitr::kable()| time | forecasted | observed |
|---|---|---|
| 2015-09-02 | 14167.49 | 13958 |
| 2015-10-02 | 14179.49 | 14064 |
| 2015-11-02 | 14122.35 | 13828 |
| 2015-12-02 | 13692.24 | 13327 |
| 2016-01-02 | 13108.59 | 12566 |
| 2016-02-01 | 13489.83 | 13406 |
| 2016-03-02 | 13710.53 | 13824 |
| 2016-04-02 | 13890.32 | 13885 |
| 2016-05-02 | 13799.82 | 13835 |
| 2016-06-02 | 13850.34 | 13763 |
| 2016-07-02 | 13901.94 | 13944 |
| 2016-08-02 | 14262.94 | 14158 |
| 2016-09-01 | 14181.94 | 14021 |
| 2016-10-01 | 14193.80 | 13862 |
| 2016-11-01 | 14136.47 | 13848 |
| 2016-12-01 | 13705.89 | 13444 |
| 2017-01-01 | 13121.66 | 13017 |
| 2017-01-31 | 13503.06 | 13211 |
| 2017-03-03 | 13723.79 | 13779 |
| 2017-04-02 | 13903.58 | 13919 |
| 2017-05-03 | 13812.88 | 13502 |
| 2017-06-02 | 13863.31 | 13815 |
| 2017-07-02 | 13914.82 | 13953 |
| 2017-08-02 | 14275.95 | 14172 |
