Capítulo 3 Regressão
library(magrittr)
library(tidyverse)
library(GGally)
library(forecast)
library(broom)
library(ggalt)
library(ggExtra)A técnica chamada de regressão é usada para predizer o valor de uma variável Y (chamada de variável resposta ou dependente) baseado em uma ou mais variáveis X (variável explanatória ou independente). Se a regressão utiliza apenas uma variável explanatória, é chamada de regressão simples. O objetivo da regressão é representar a relação entre as variáveis resposta e explanatória por meio de uma equação matemática linear do tipo:
$Y = _1 + _2X + $
onde \(\beta_1\) é a interceptação da reta com o eixo vertical e \(\beta_2\) o coeficiente de inclinação associado à variável explanatória. Tais elementos são chamados coeficientes da regressão. O termo \(\epsilon\) representa o termo do erro, que é a parte de Y que a regressão é incapaz de explicar (por existir outras variáveis que explicariam Y mas que não foram incorporadas ao modelo).
Neste capítulo, usaremos como exemplo o dataset x15 extraído deste site, que traz dados que tentam explicar o consumo de petróleo baseado em outros inputs. Os dados não vêm já formatados, o que vai acabar servindo para mostrar um exemplo de limpeza de dados em R.
url <- "http://people.sc.fsu.edu/~jburkardt/datasets/regression/x15.txt"
readLines(url)## [1] "# x15.txt"
## [2] "#"
## [3] "# Reference:"
## [4] "#"
## [5] "# Helmut Spaeth,"
## [6] "# Mathematical Algorithms for Linear Regression,"
## [7] "# Academic Press, 1991,"
## [8] "# ISBN 0-12-656460-4."
## [9] "#"
## [10] "# S Weisberg,"
## [11] "# Applied Linear Regression,"
## [12] "# New York, 1980, pages 32-33."
## [13] "#"
## [14] "# Discussion:"
## [15] "#"
## [16] "# For one year, the consumption of petrol was measured in 48 states."
## [17] "# The relevant variables are the petrol tax, the average"
## [18] "# income per capita, the number of miles of paved highway, and"
## [19] "# the proportion of the population with driver's licenses."
## [20] "#"
## [21] "# There are 48 rows of data. The data include:"
## [22] "#"
## [23] "# I, the index;"
## [24] "# A1, the petrol tax;"
## [25] "# A2, the per capita income;"
## [26] "# A3, the miles of paved highway;"
## [27] "# A4, the proportion of drivers;"
## [28] "# B, the consumption of petrol."
## [29] "#"
## [30] "# We seek a model of the form:"
## [31] "#"
## [32] "# B = A1 * X1 + A2 * X2 + A3 * X3 + A4 * X4."
## [33] "#"
## [34] "6 columns"
## [35] "48 rows"
## [36] "Index"
## [37] "Petrol tax (cents per gallon)"
## [38] "Average income (dollars)"
## [39] "Paved Highways (miles)"
## [40] "Proportion of population with driver's licenses"
## [41] "Consumption of petrol (millions of gallons)"
## [42] " 1 9.00 3571 1976 0.5250 541"
## [43] " 2 9.00 4092 1250 0.5720 524"
## [44] " 3 9.00 3865 1586 0.5800 561"
## [45] " 4 7.50 4870 2351 0.5290 414"
## [46] " 5 8.00 4399 431 0.5440 410"
## [47] " 6 10.00 5342 1333 0.5710 457"
## [48] " 7 8.00 5319 11868 0.4510 344"
## [49] " 8 8.00 5126 2138 0.5530 467"
## [50] " 9 8.00 4447 8577 0.5290 464"
## [51] "10 7.00 4512 8507 0.5520 498"
## [52] "11 8.00 4391 5939 0.5300 580"
## [53] "12 7.50 5126 14186 0.5250 471"
## [54] "13 7.00 4817 6930 0.5740 525"
## [55] "14 7.00 4207 6580 0.5450 508"
## [56] "15 7.00 4332 8159 0.6080 566"
## [57] "16 7.00 4318 10340 0.5860 635"
## [58] "17 7.00 4206 8508 0.5720 603"
## [59] "18 7.00 3718 4725 0.5400 714"
## [60] "19 7.00 4716 5915 0.7240 865"
## [61] "20 8.50 4341 6010 0.6770 640"
## [62] "21 7.00 4593 7834 0.6630 649"
## [63] "22 8.00 4983 602 0.6020 540"
## [64] "23 9.00 4897 2449 0.5110 464"
## [65] "24 9.00 4258 4686 0.5170 547"
## [66] "25 8.50 4574 2619 0.5510 460"
## [67] "26 9.00 3721 4746 0.5440 566"
## [68] "27 8.00 3448 5399 0.5480 577"
## [69] "28 7.50 3846 9061 0.5790 631"
## [70] "29 8.00 4188 5975 0.5630 574"
## [71] "30 9.00 3601 4650 0.4930 534"
## [72] "31 7.00 3640 6905 0.5180 571"
## [73] "32 7.00 3333 6594 0.5130 554"
## [74] "33 8.00 3063 6524 0.5780 577"
## [75] "34 7.50 3357 4121 0.5470 628"
## [76] "35 8.00 3528 3495 0.4870 487"
## [77] "36 6.58 3802 7834 0.6290 644"
## [78] "37 5.00 4045 17782 0.5660 640"
## [79] "38 7.00 3897 6385 0.5860 704"
## [80] "39 8.50 3635 3274 0.6630 648"
## [81] "40 7.00 4345 3905 0.6720 968"
## [82] "41 7.00 4449 4639 0.6260 587"
## [83] "42 7.00 3656 3985 0.5630 699"
## [84] "43 7.00 4300 3635 0.6030 632"
## [85] "44 7.00 3745 2611 0.5080 591"
## [86] "45 6.00 5215 2302 0.6720 782"
## [87] "46 9.00 4476 3942 0.5710 510"
## [88] "47 7.00 4296 4083 0.6230 610"
## [89] "48 7.00 5002 9794 0.5930 524"
## [90] ""# Os dados de verdade estão presentes entre as linhas 42 a 89.
# Os nomes das colunas estão presentes entre as linhas 36 a 41
dados <- readLines(url)[42:89]
# como salvamos o dataset como se fosse um string em uma variavel...
# (ao inves de importar de um arquivo de texto), precisamos indicar que a variavel...
# dados corresponde a um arquivo de texto que contem um dataset
con <- textConnection(dados)
df <- read.table(con, header = FALSE)
close(con)
# adicionando o nome das colunas
names(df) <- c("linha", "imposto", "renda_media", "km_asfaltado", "n_carteiras",
"consumo")
# retirar a primeira coluna já que nao serve para nada
df <- df[,-1]
head(df)## imposto renda_media km_asfaltado n_carteiras consumo
## 1 9.0 3571 1976 0.525 541
## 2 9.0 4092 1250 0.572 524
## 3 9.0 3865 1586 0.580 561
## 4 7.5 4870 2351 0.529 414
## 5 8.0 4399 431 0.544 410
## 6 10.0 5342 1333 0.571 457O objetivo aqui é descobrir qual das 4 variáveis explica a variável consumo.
3.1 Correlação
Correlação é um indicador estatístico que mede o nível de dependência linear entre duas variáveis. Está definida no intervalo [-1, +1]. Se a correlação é negativa, indica que as variáveis são inversamente proporcinais: quando uma aumenta, a outra diminui. Se é positiva, indica que as variáveis são diretamente proporcionais.
Medir a correlação no R é muito simples:
# Usando a função cor
cor(df$consumo, df$n_carteiras)## [1] 0.6989654cor(df$consumo, df$renda_media)## [1] -0.2448621Para analisar todas as correlações entre todas as variáveis de uma só vez, podemos tanto calcular uma matriz de correlação como plotar todas as correlações com o auxílio do pacote GGally:
# matriz de correlacao:
cor(df)## imposto renda_media km_asfaltado n_carteiras consumo
## imposto 1.00000000 0.01266516 -0.52213014 -0.2880372 -0.45128028
## renda_media 0.01266516 1.00000000 0.05016279 0.1570701 -0.24486207
## km_asfaltado -0.52213014 0.05016279 1.00000000 -0.0641295 0.01904194
## n_carteiras -0.28803717 0.15707008 -0.06412950 1.0000000 0.69896542
## consumo -0.45128028 -0.24486207 0.01904194 0.6989654 1.00000000# usando o pacote GGally
ggpairs(df)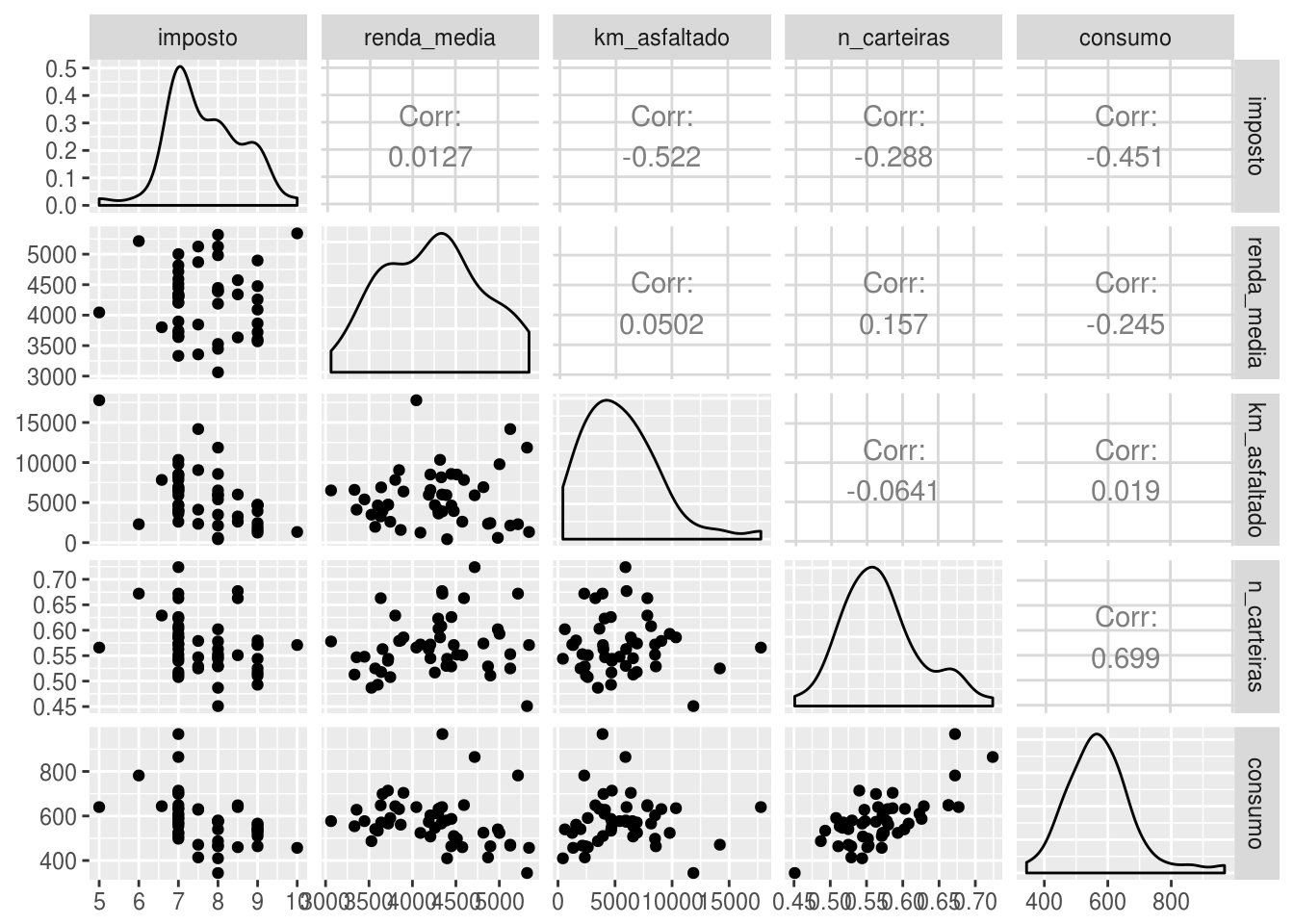
Percebe-se pela matriz de correlação (e principalmente pelo gráfico) que só valeria a pena usar como variáveis explanatórias do nosso objeto de estudo o número de carteiras de habilitação e talvez o imposto sobre o consumo de petróleo.
3.2 Análise explatória e gráfica
No gráfico acima, mais precisamente na parte referente ao gráfico de dispersão entre as variáveis consumo e número de carteiras, é notório que existem quatro pontos que se destacam dos demais: três para cima e um para baixo. Como eles estão distantes verticalmente do “bolo” de pontos, o que é um indício de que são outliers em consumo. Tratamento de outliers é um tópico fundamental na construção de modelos.
Primeiramente, vamos analisar a distribuição da variável de consumo por meio de um histograma:
# pelo ggplot2, o grafico fica com intervalos meio feios:
ggplot(df, aes(x = consumo)) +
geom_histogram() +
labs(x = "Consumo", y = "Quantidade")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.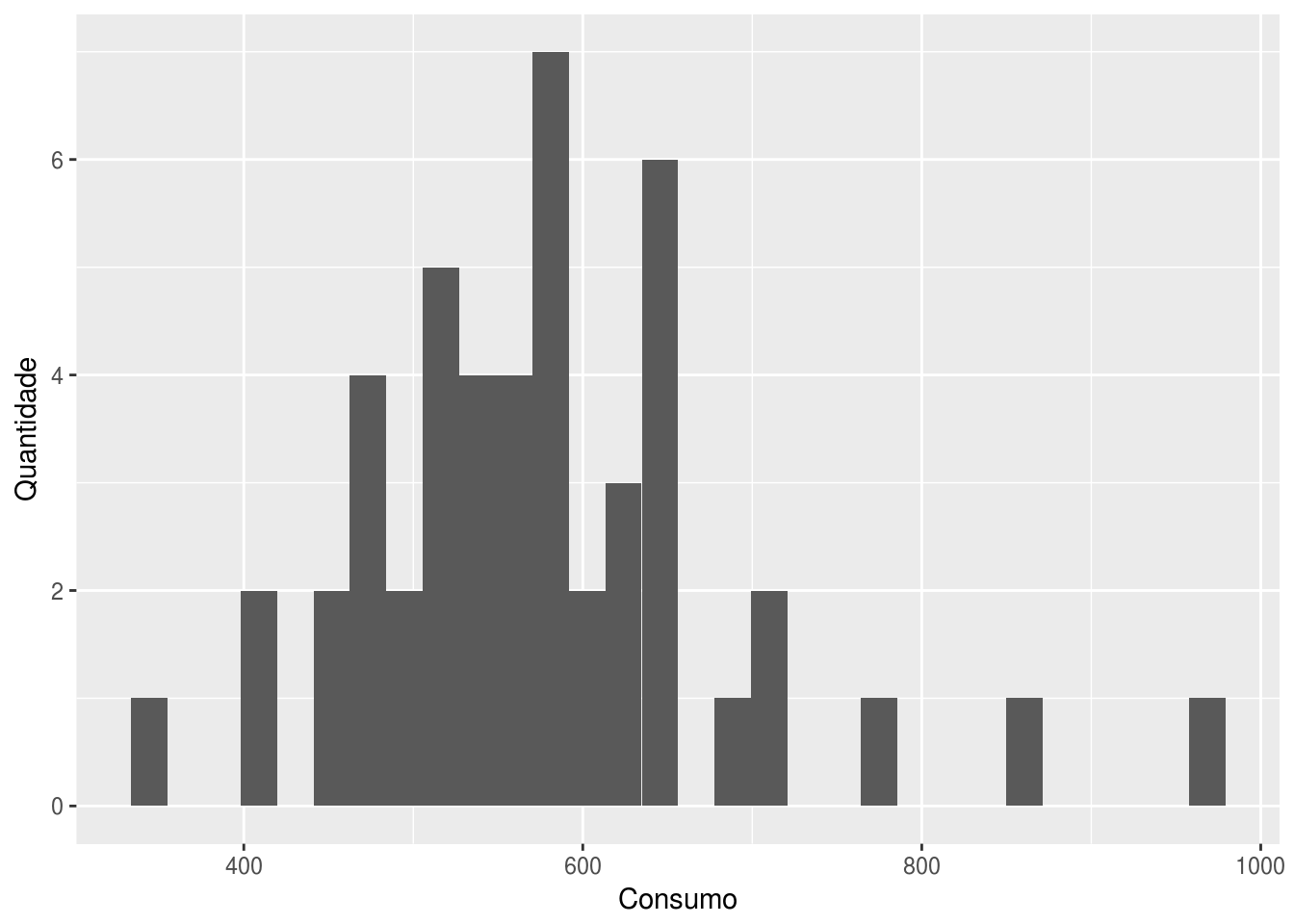
# o pacote forecast traz uma versao melhorada do histograma do ggplot2:
gghistogram(df$consumo) +
labs(x = "Consumo", y = "Quantidade")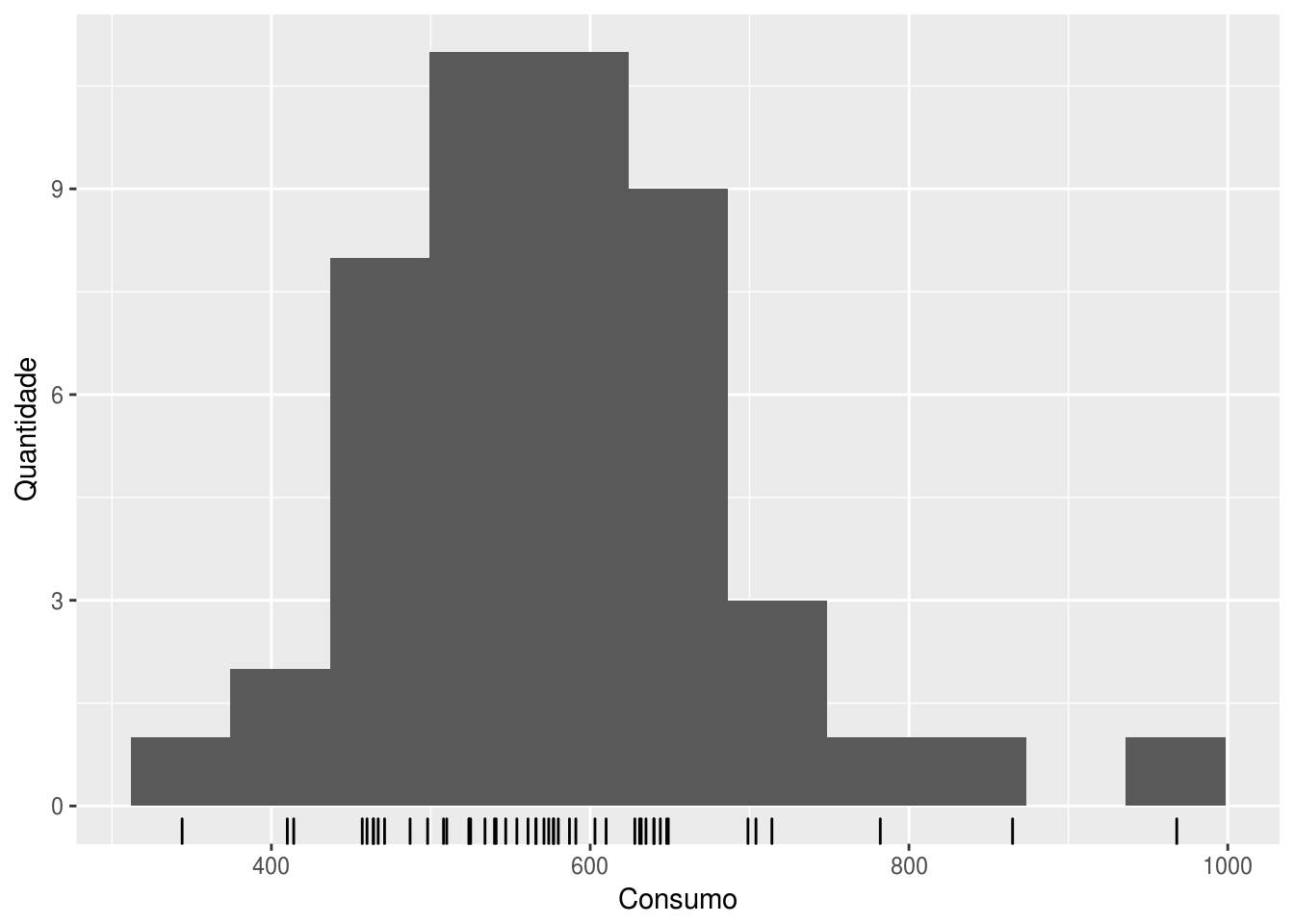
O histograma confirma que os valores acima de 800 peças e abaixo de 400 são anomalias dada a distribuição normal que a variável consumo aparenta ter.
Visto que é possível descrever consumo como uma distribuição normal, pode-se assumir que a probabilidade de que um valor esteja fora do intervalo \(\mu(consumo) \pm 3 \times \sigma(consumo)\) é de apenas 0,27%. Vamos destacar esses outliers com o auxílio dos pacotes ggalt e ggExtra, que são extensões do ggplot2.
# calcular limites superior e inferior
lim_sup <- mean(df$consumo) + 2 * sd(df$consumo)
lim_inf <- mean(df$consumo) - 2 * sd(df$consumo)
# por curiosidade, como ficaria com o pipe:
lim_sup <- df$consumo %>% {mean(.) + 3 * sd(.)}
lim_inf <- df$consumo %>% {mean(.) - 3 * sd(.)}
# criar dataframe sem outliers
df_sem_out <- df %>% filter(lim_inf < consumo & consumo < lim_sup)
p <- ggplot(df, aes(x = n_carteiras, y = consumo)) +
geom_point() +
# adicionar curva da regressao
geom_smooth(method = "lm") +
# plotar circulo que deixe de fora os outliers
geom_encircle(data = df_sem_out,
aes(x = n_carteiras, y = consumo), color = 'red') +
labs(x = "Número de carteiras de motorista", y = "Consumo de petróleo")
# plotar histogramas nas margens do grafico
ggMarginal(p, type = "histogram")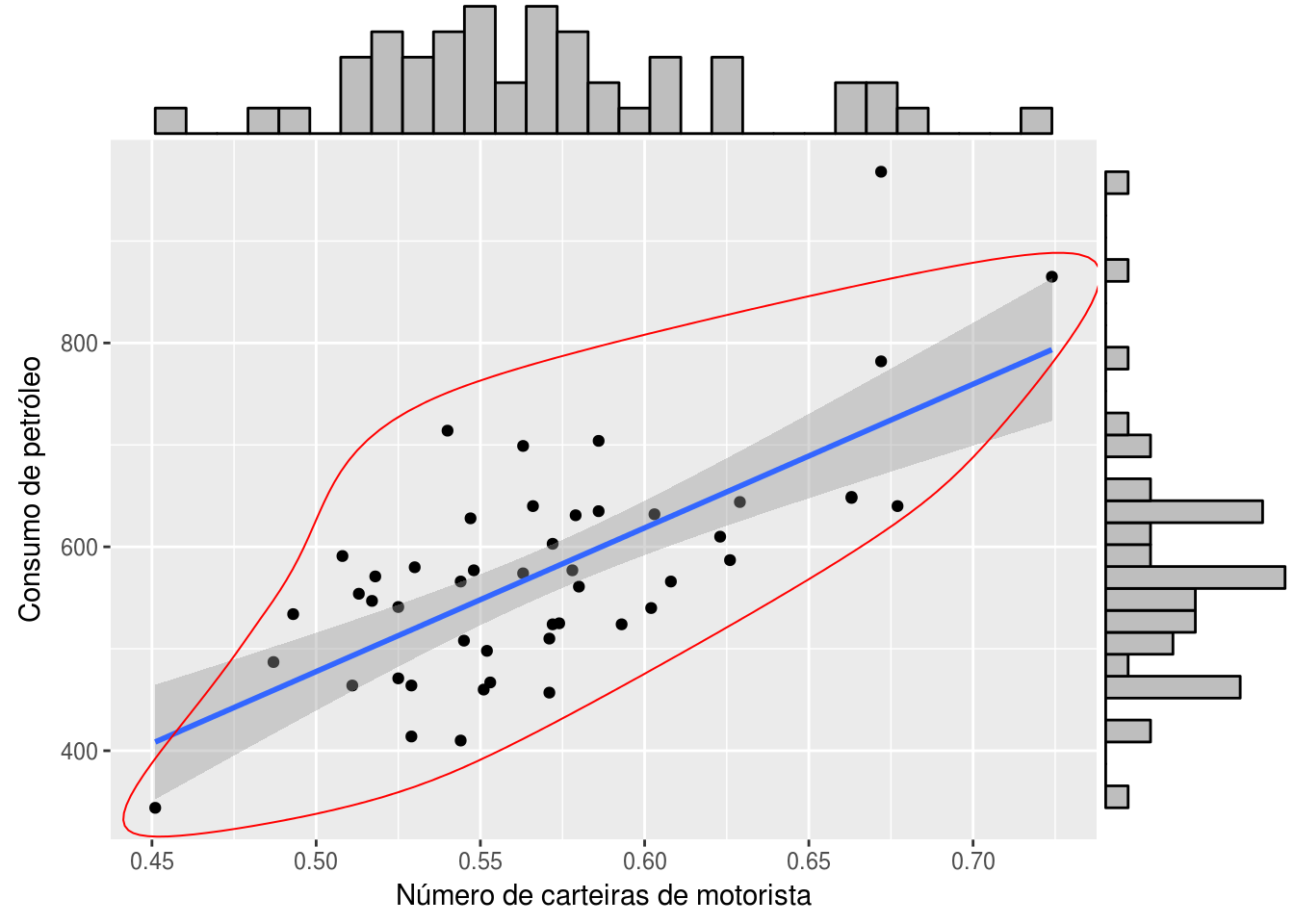
Agora o outlier onde consumo > 800 e n_carteiras > 0,65 ficou mais visível. Portanto, faz sentido removê-lo da análise.
Como ficam as correlacões sem o outlier?
# comparar as matrizes de correlacao
cor(df)## imposto renda_media km_asfaltado n_carteiras consumo
## imposto 1.00000000 0.01266516 -0.52213014 -0.2880372 -0.45128028
## renda_media 0.01266516 1.00000000 0.05016279 0.1570701 -0.24486207
## km_asfaltado -0.52213014 0.05016279 1.00000000 -0.0641295 0.01904194
## n_carteiras -0.28803717 0.15707008 -0.06412950 1.0000000 0.69896542
## consumo -0.45128028 -0.24486207 0.01904194 0.6989654 1.00000000cor(df_sem_out)## imposto renda_media km_asfaltado n_carteiras consumo
## imposto 1.00000000 0.01550113 -0.53357179 -0.27154780 -0.46681324
## renda_media 0.01550113 1.00000000 0.05216791 0.15575222 -0.30179781
## km_asfaltado -0.53357179 0.05216791 1.00000000 -0.04705121 0.06454609
## n_carteiras -0.27154780 0.15575222 -0.04705121 1.00000000 0.67838583
## consumo -0.46681324 -0.30179781 0.06454609 0.67838583 1.000000003.3 Modelagem por regressão simples
No R, é bem simples ajustar um modelo de regressão. Usando a variável n_carteiras como explanatória e consumo como resposta, um modelo é construído da seguinte maneira:
modelo.simples <- lm(consumo ~ n_carteiras, data = df_sem_out)
summary(modelo.simples)##
## Call:
## lm(formula = consumo ~ n_carteiras, data = df_sem_out)
##
## Residuals:
## Min 1Q Median 3Q Max
## -129.011 -51.414 -3.418 51.053 179.860
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -123.5 112.2 -1.101 0.277
## n_carteiras 1217.8 196.6 6.194 1.61e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 71.99 on 45 degrees of freedom
## Multiple R-squared: 0.4602, Adjusted R-squared: 0.4482
## F-statistic: 38.37 on 1 and 45 DF, p-value: 1.608e-07Com o modelo criado, é possível descrever a relação entre consumo e n_carteiras matematicamente por meio da seguinte equação:
\(consumo = -123.5 + 1217.8 \times n\_carteiras\)
Vamos deixar para analisar os diagnósticos da regressão no próximo item:
3.4 Regressão multivariada
Suponha também que você deseja incorporar a variável imposto ao modelo. Antes de fazer isso, vamos ver como as duas variáveis explanatórias se relacionam com a resposta em um gráfico tridimensional:
ggplot(df, aes(x = n_carteiras, y = consumo, color = imposto)) +
geom_point() +
scale_color_continuous(low = "green", high = "red")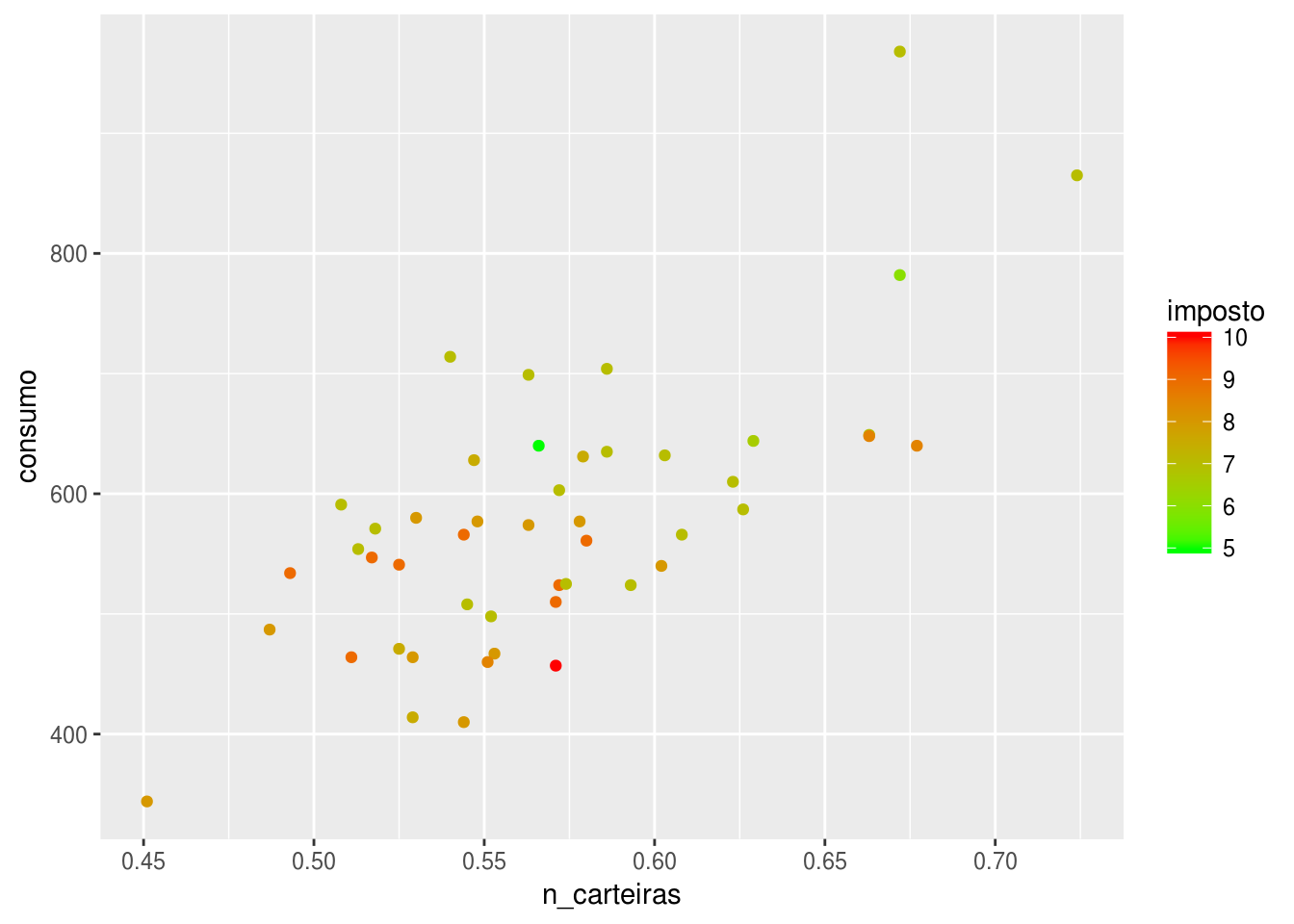
Valores altos de impostos aparentam estar associados com valores baixos de consumo.
Para adicionar uma nova variável ao modelo, fazemos:
modelo.mult <- lm(consumo ~ n_carteiras + imposto, data = df_sem_out)
summary(modelo.mult)##
## Call:
## lm(formula = consumo ~ n_carteiras + imposto, data = df_sem_out)
##
## Residuals:
## Min 1Q Median 3Q Max
## -122.786 -55.792 3.455 47.914 154.557
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 198.65 152.41 1.303 0.19920
## n_carteiras 1069.12 189.39 5.645 1.12e-06 ***
## imposto -30.93 10.70 -2.892 0.00593 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 66.74 on 44 degrees of freedom
## Multiple R-squared: 0.5464, Adjusted R-squared: 0.5258
## F-statistic: 26.5 on 2 and 44 DF, p-value: 2.794e-08# Usando o pacote broom para formatar o output dos modelos de regressao
# concatenando os dois modelos em um dataframe so
# metricas dos regressores
modelo.simples %>% tidy## term estimate std.error statistic p.value
## 1 (Intercept) -123.4979 112.2050 -1.100646 2.769038e-01
## 2 n_carteiras 1217.8476 196.6181 6.193976 1.608027e-07modelo.mult %>% tidy## term estimate std.error statistic p.value
## 1 (Intercept) 198.65147 152.40539 1.303441 1.992035e-01
## 2 n_carteiras 1069.11730 189.38537 5.645195 1.118216e-06
## 3 imposto -30.93311 10.69589 -2.892056 5.928055e-03# metricas do modelo
rbind(modelo.simples %>% glance,
modelo.mult %>% glance)## r.squared adj.r.squared sigma statistic p.value df logLik
## 1 0.4602073 0.4482119 71.99031 38.36534 1.608027e-07 2 -266.6652
## 2 0.5464273 0.5258103 66.73658 26.50380 2.794040e-08 3 -262.5755
## AIC BIC deviance df.residual
## 1 539.3304 544.8808 233217.2 45
## 2 533.1510 540.5516 195965.9 44Agora vamos à análise dos indicadores da regressão:
3.4.1 Hipótese nula da regressão
A presença de um valor-p indica que existe uma hipótese nula sendo testada. Na regressão linear, a hipótese nula é a de que os coeficientes das variáveis explanatórias são iguais a zero. A hipótese alternativa é a de que os coeficientes não são iguais a zero, ou seja, existe uma relação matemático entre as variáveis do modelo.
3.4.2 valor-p
Nós podemos considerar um modelo linear estatisticamente significante apenas se os valores-p, tanto dos coeficientes como do modelo, são menores que um nível de significância pré-determinado, que idealmente é 0,05.
3.4.3 valor-t ou estatística
Um valor grande do valor-t indica que é pouco provável que os coeficientes não sejam iguais a zero puramente por coincidência. Assim, quanto maior o valor-t, melhor.
3.4.4 R-quadrado e R-quadrado ajustado
R-quadrado é a proporção da variação da variável resposta que é explicada pelo modelo. Quanto maior, melhor o modelo, supostamente.
Se continuarmos adicionando variáveis ao modelo de regressão, o R-quadrado apenas tende a crescer, intuitivamente. Isso acontecerá mesmo que a variável explanatória adicionada não seja significante. Para evitar esse problema que tornaria a comparação entre modelos praticamente inviável, o R-quadrado ajustado “penaliza” o valor do R-quadrado pelo número de variáveis adicionadas. Semelhantemente ao R-quadrado, quanto maior, melhor.
3.4.5 AIC e BIC
O AIC (Critério de Informação de Akaike) e o BIC (Critério de Informação Bayesiano) são métricas de qualidade de ajuste de um modelo estatístico que podem ser usados para a seleção de modelos. Quanto menor os valores, melhor o modelo.
3.4.6 Análise dos resíduos
Um indicador visual da qualidade de um modelo é a distribuição dos modelos: um bom modelo apresentará resídos que seguem uma distribuição normal com média 0.
Um modelo de regressão pressupõe que seus resíduos (subtração entre o valor real e o ajustado) seguem uma distribuição normal e não possuem nenhum tipo de relação matemática com os regressores do modelo (ou mesmo com variáveis independentes não usadas no modelo).
Para analisar o primeiro pressuposto do modelo múltiplo, fazemos um histograma dos resíduos:
modelo.mult$residuals %>% hist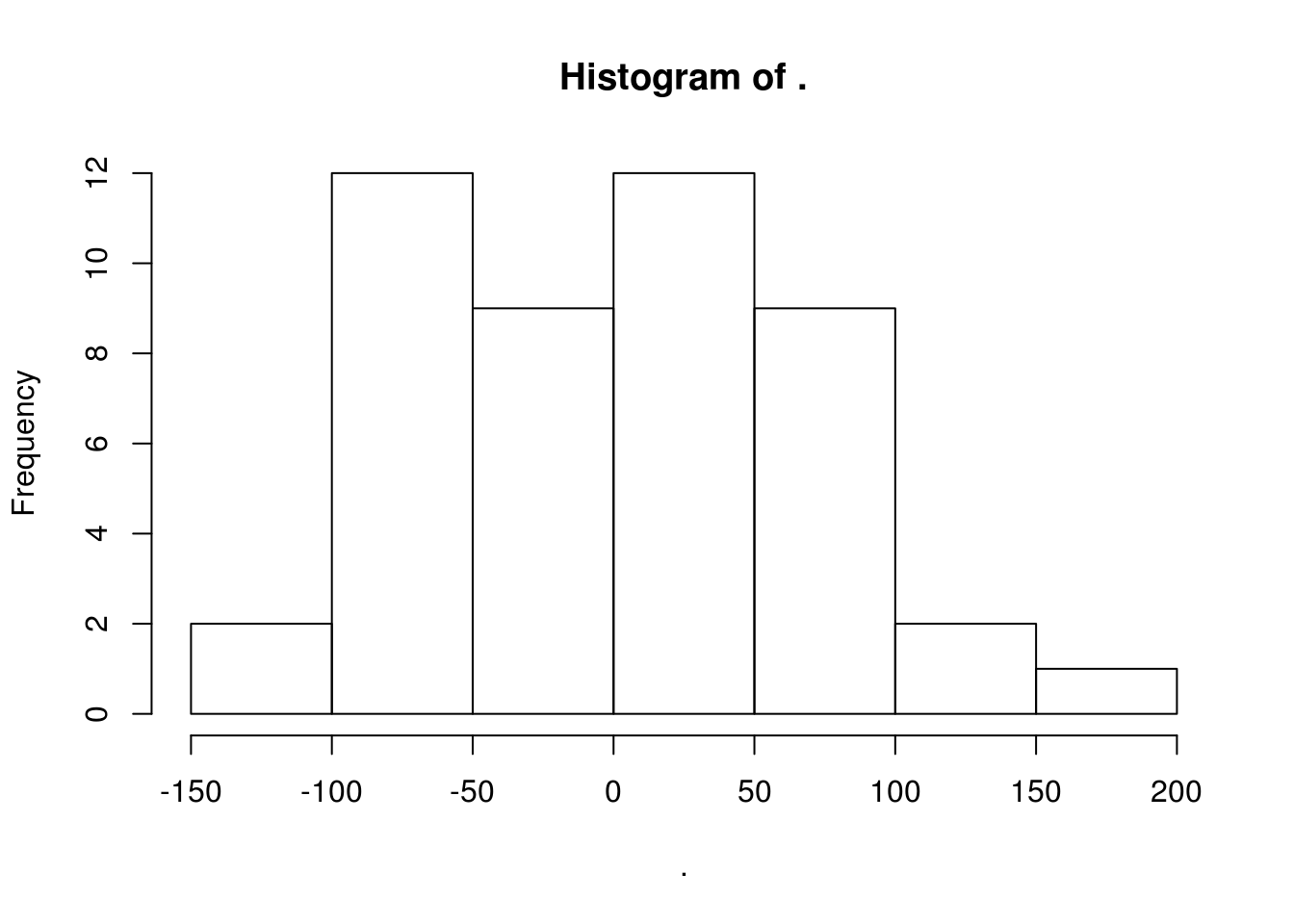
Para analisar o segundo pressuposto, plotamos os resíduos contra todas as variáveis do dataset:
par(mfrow=c(2,2))
plot(df_sem_out$imposto, residuals(modelo.mult), xlab = "imposto")
plot(df_sem_out$renda_media, residuals(modelo.mult), xlab = "renda media")
plot(df_sem_out$km_asfaltado, residuals(modelo.mult), xlab = "km asfaltado")
plot(df_sem_out$n_carteiras, residuals(modelo.mult), xlab = "n_carteiras")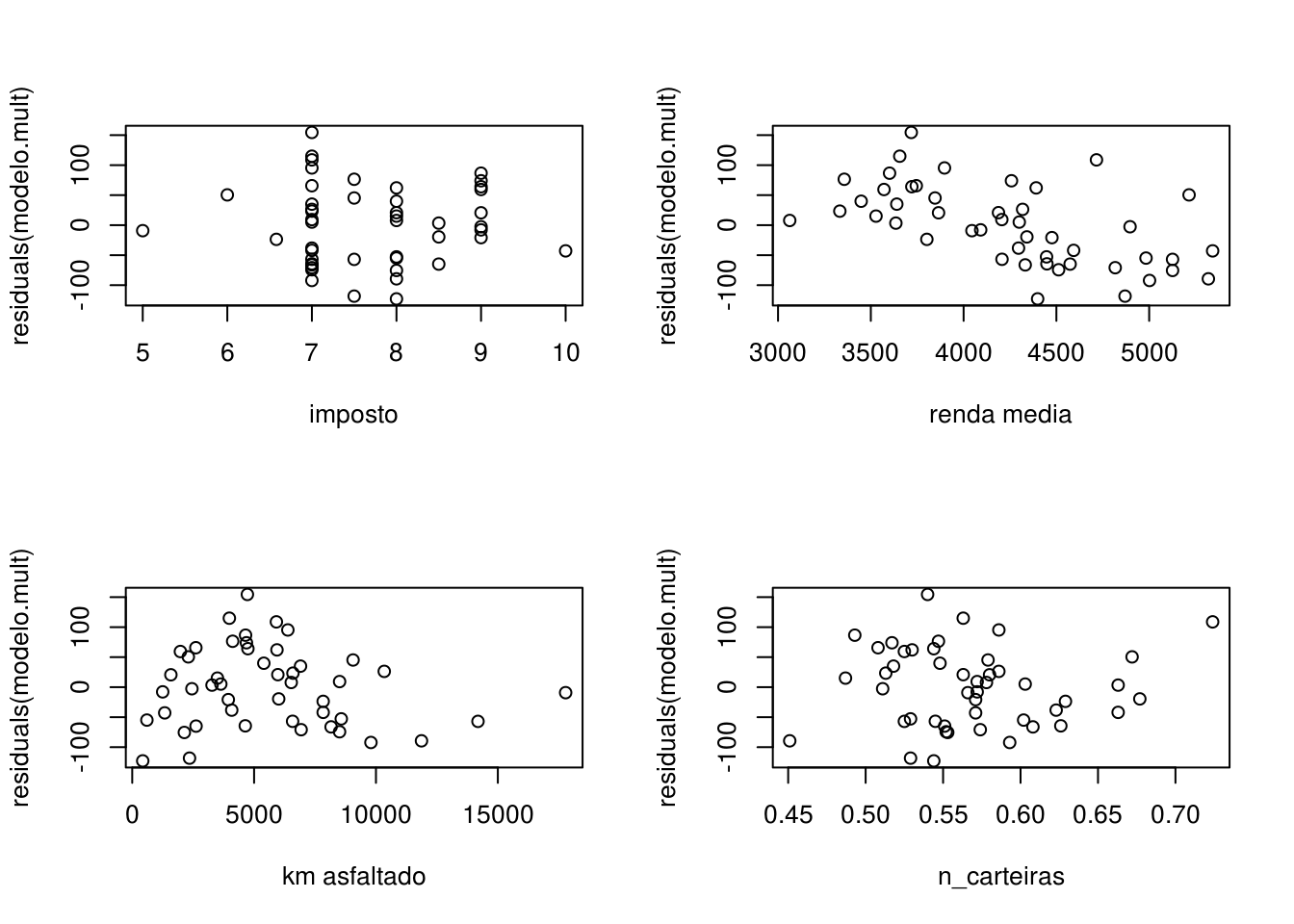
Os resíduos do modelo múltiplo aparentam ter alguma relação com a variável renda_media, o que indica que ela pode ser incorporada ao modelo.
3.5 Regressão como modelo preditivo
Um dos objetivos da regressão, além de descrever matematicamente a relação entre duas ou mais variáveis, é prever o valor da variável dependente baseado em novos valores da variável independente. Não é possível afirmar que um modelo apresentará um bom desempenho preditivo analisando apenas as métricas da regressão do tópico anterior. É necessário testar o modelo em dados que ele nunca viu.
A prática comum em Data Science é de separar o conjunto de dados que se tem em mãos em dois conjuntos: o de treino, que será usado para construir o modelo, e o de teste, que será usado como input do modelo para avaliar sua acurácia.
Após obter as previsões, deve-se usar uma ou mais métricas de erro (ver capítulo posterior) para avaliar a precisão do modelo.
set.seed(1993) # escolhendo uma seed para tornar os resultados previsiveis
indice <- sample(1:nrow(df_sem_out), 0.8*nrow(df_sem_out)) # row indices for training data
treino <- df_sem_out[indice, ] # model training data
teste <- df_sem_out[-indice, ] # test data
# construindo os dois modelos, mantendo o teste de fora
modelo.simples <- lm(consumo ~ n_carteiras, data = treino)
modelo.mult <- lm(consumo ~ n_carteiras + imposto, data = treino)
# calcular previsao baseado no dataframe de teste
prev.simples <- predict(modelo.simples, teste)
prev.mult <- predict(modelo.mult, teste)
# uma das metricas é correlação entre previsto e real:
real = teste$consumo
cor(prev.simples, real)## [1] 0.8841406cor(prev.mult, real)## [1] 0.8611087# outra metrica é o MAPE
mean(abs(prev.simples - real)/real)## [1] 0.1101031mean(abs(prev.mult - real)/real)## [1] 0.1134987Os dois modelos apresentam resultados semelhantes de erro. Portanto, pelo menos para este teste, não houve um aumento significativo de acurácia no modelo ao incorporar a variável imposto como explanatória.
